
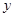 轴于点F,其中点E的横坐标为-2,若直线
轴于点F,其中点E的横坐标为-2,若直线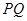 为抛物线的对称轴,点G为直线
为抛物线的对称轴,点G为直线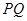 上的一动点,则
上的一动点,则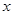 轴上是否存在一点H,使
轴上是否存在一点H,使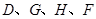 四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;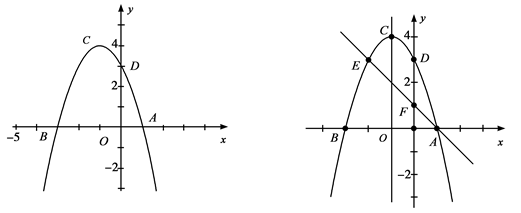

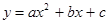 ,将A(1,0)、B(-3,0)、 D(0,3)代入,得
,将A(1,0)、B(-3,0)、 D(0,3)代入,得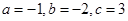 …………………………………………2分
…………………………………………2分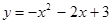 ……………………………3分
……………………………3分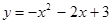 ,得
,得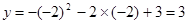
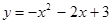 图象分别与x轴、y轴交于点A(1,0)、B(-3,0)、
图象分别与x轴、y轴交于点A(1,0)、B(-3,0)、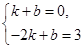 解得:
解得: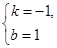
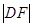 =2………………………………………③
=2………………………………………③ 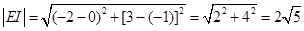 ……………………………………④
……………………………………④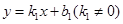 ,
,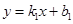 ,得:
,得: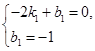 解得:
解得: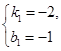
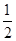 ;
; 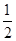 ,0)
,0)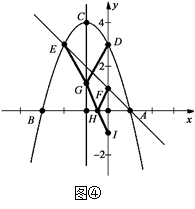
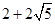
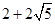 . …………………………………………7分
. …………………………………………7分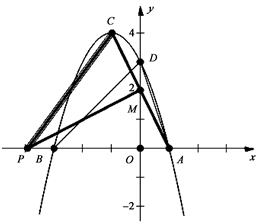
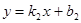 ,得:
,得: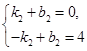
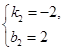 ,
,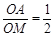 , ………………8分
, ………………8分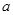 ,0),CM=
,0),CM=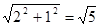 ,且∠CPM不可能为90°时,因此可分两种情况讨论; ……………………………………………………………………………9分
,且∠CPM不可能为90°时,因此可分两种情况讨论; ……………………………………………………………………………9分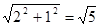 ,若
,若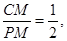 则
则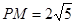 ,可求的P(-4,0),则CP=5,
,可求的P(-4,0),则CP=5,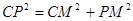 ,即P(-4,0)成立,若
,即P(-4,0)成立,若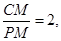 由图可判断不成立;……………………………………………………………………………………10分
由图可判断不成立;……………………………………………………………………………………10分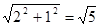 ,若
,若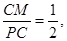 则
则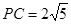 ,可求出
,可求出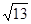 ,显然不成立,若
,显然不成立,若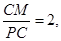 则
则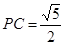 ,更不可能成立.……11分
,更不可能成立.……11分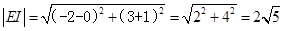 ,DF+EI=
,DF+EI=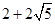
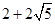 .
. 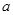 ,0),CM=
,0),CM=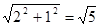 ,且∠CPM不可能为90°时,因此可分两种情况讨论,①当∠CMP=90°时,CM=
,且∠CPM不可能为90°时,因此可分两种情况讨论,①当∠CMP=90°时,CM=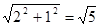 ,若
,若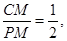 则
则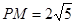 ,可求的P(-4,0),则CP=5,
,可求的P(-4,0),则CP=5,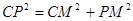 ,即P(-4,0)成立,若
,即P(-4,0)成立,若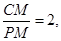 由图可判断不成立;②当∠PCM=90°时,CM=
由图可判断不成立;②当∠PCM=90°时,CM=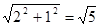 ,若
,若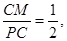 则
则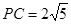 ,可求出P(-3,0),则PM=
,可求出P(-3,0),则PM=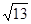 ,显然不成立,若
,显然不成立,若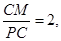 则
则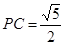 ,更不可能成立. 即求出以P、C、M为顶点的三角形与△AOM相似的P的坐标(-4,0)
,更不可能成立. 即求出以P、C、M为顶点的三角形与△AOM相似的P的坐标(-4,0) 

科目:初中数学 来源: 题型:
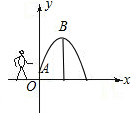 如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则这个二次函数的表达式为
如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,球路的最高点B(8,9),则这个二次函数的表达式为查看答案和解析>>
科目:初中数学 来源: 题型:
如图2,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1 m,球路的最高点B(8,9),则这个二次函数的表达式为______,小孩将球抛出了约______米(精确到0.1 m).
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011届河南省周口市初三下册26章《二次函数》检测题 题型:填空题
如图2,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1 m,球路的最高点B(8,9),则这个二次函数的表达式为______,小孩将球抛出了约______米(精确到0.1 m).
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南省周口市初三下册26章《二次函数》检测题 题型:填空题
如图2,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1 m,球路的最高点B(8,9),则这个二次函数的表达式为______,小孩将球抛出了约______米(精确到0.1 m).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com