解:(1)∵AC⊥BC,OC⊥AB,
∴△AOC∽△COB,
∴

=

∵AO=1.8,则OC=2.4,
∴

=

解得OB=3.2,
∴点B的坐标为(3.2,0)
设经过点A、B、C的抛物线的解析式为y=ax
2+bx+c,
将点A、B、C的坐标代入得y=-


x

(2)用勾股定理求出AC=3,BC=4,
∵AC⊥BC,MN∥AC,MP∥BC,
∴四边形MNCP为矩形,且△MNB∽△ACB,

=

设MN=3x,则NB=4x,得CN=4-4x
∴四边形MNCP的面积为3x(4-4x),从而△MNP的面积是:
S=

3x(4-4x)
=-6x
2+6x
=-6(x-

)
2+

当x=

,△MNP面积的最大值为

;
(3)∵l∥AB,
∴△ABC的面积(2)中△ABC的面积相等为6,
由MN∥AC,MP∥BC,得△MNB∽△ACB,△MAP∽△BAC
则

=

,

=

设MB=x,则AM=5-x,
∴△MBN的面积是;
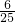
x
2,△MAP的面积是:

,
∴△MNP的面积是:
S=

(△ABC的面积-△MBN的面积-△MAP的面积)
=-

+

x
=-
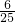
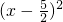
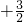
,
当x=

,即MB为

时,△MNP面积的最大值为

,
∴(2)中的结论仍然成立.
分析:(1)本题须先证出△AOC∽△COB,从而得出点B的坐标,再把点A、B、C的坐标代入即可求出抛物线的解析式.
(2)本题须先根据△MNB∽△ACB,得出

=

,再表示出CN的长,然后代入四边形MNCP的面积为3x(4-4x),从而得出S=-6(x-

)
2+

,即可求出
△MNP面积的最大值为.
(3)本题须先根据相似三角形的性质得出则△MNP的面积,然后求出△MNP面积的最大值即可得出正确结论.
点评:本题主要考查了二次函数的综合应用,在解题时要注意把二次函数的图象和性质与相似三角形的性质相结合是本题的关键.


 =
=
 =
=

 x
x
 =
=
 3x(4-4x)
3x(4-4x) )2+
)2+
 ,△MNP面积的最大值为
,△MNP面积的最大值为 ;
; =
= ,
, =
=
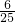 x2,△MAP的面积是:
x2,△MAP的面积是: ,
, (△ABC的面积-△MBN的面积-△MAP的面积)
(△ABC的面积-△MBN的面积-△MAP的面积) +
+ x
x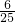
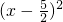
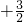 ,
, ,即MB为
,即MB为 时,△MNP面积的最大值为
时,△MNP面积的最大值为 ,
, =
= ,再表示出CN的长,然后代入四边形MNCP的面积为3x(4-4x),从而得出S=-6(x-
,再表示出CN的长,然后代入四边形MNCP的面积为3x(4-4x),从而得出S=-6(x- )2+
)2+ ,即可求出
,即可求出

 一课一练课时达标系列答案
一课一练课时达标系列答案