
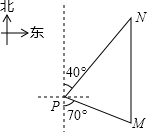
 如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为
如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
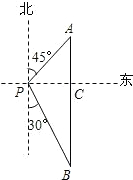 如图,一艘海轮位于灯塔P的东北方向,距离灯塔40
如图,一艘海轮位于灯塔P的东北方向,距离灯塔40| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
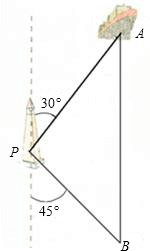 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔30海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?A、B两处相距多远?(取
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔30海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的东南方向上的B处.这时,海轮所在的B处距离灯塔P有多远?A、B两处相距多远?(取| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
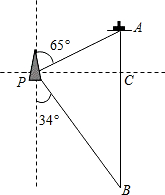 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到1海里,参考数据:cos25°≈0.91,sin25°≈0.42,tan25°≈0.47,sin34°≈0.56,cos34°≈0.83,tan34°≈0.67 )
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到1海里,参考数据:cos25°≈0.91,sin25°≈0.42,tan25°≈0.47,sin34°≈0.56,cos34°≈0.83,tan34°≈0.67 )查看答案和解析>>
科目:初中数学 来源: 题型:
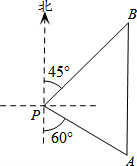 如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.
如图,一艘海轮位于灯塔P的南偏东60°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.| 2 |
| 3 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com