
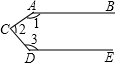 如图,AB∥DE,那么图中∠1+∠2+∠3等于
如图,AB∥DE,那么图中∠1+∠2+∠3等于 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:2013-2014学年浙江省杭州市江干区九年级上学期期末数学试卷(解析版) 题型:解答题
小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题:
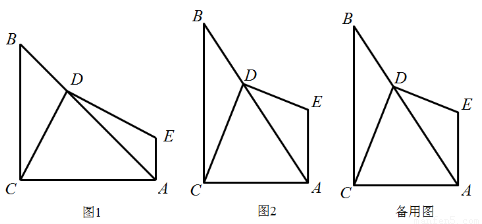
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com