解:(1)由题意可知:M点的坐标为(
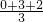
,

),
即M(

,

);
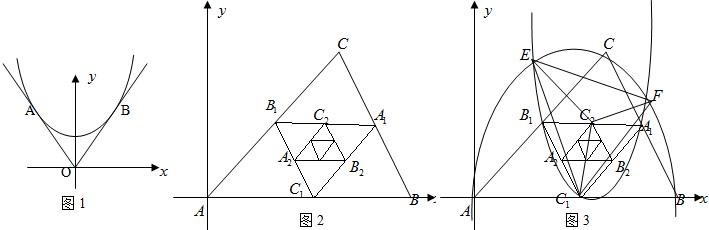
(2)设过A、B、C三点的抛物线的解析式为y=a(x-0)(x-3),
则有:2=a×(2-0)×(2-3),解得a=-1,
因此过A、B、C三点的抛物线的解析式为y=-x
2+3x,
可求得A
1、B
1、C
1的坐标分别为A
1(

,1),B
1(1,1),C
1(

,0),
设过这三点的抛物线的解析式为y=ax
2+bx+c,则有:
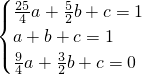
解得:
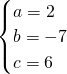
即A
1,B
1,C
1三点的抛物线解析式为y=2x
2-7x+6;
(3)根据题意有:2x
2-7x+6=-x
2+3x
即3x
2-10x+6=0
解得x=
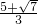
,x=
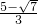
由于E在F点左侧,
因此E(
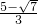
,

),F(
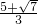
,
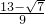
)
由题意可知C
2的坐标为(

,1)
然后将C
2的坐标代入△EFC
1三边所在的直线中,可得出C
2在△EFC
1外;
(4)A,A
2,C,C
2四点的坐标分别为:(0,0),(

,0)(2,2)(

,1),
设过A、A
2、C三点的抛物线的解析式为y=m(x-0)(x-

),
则有2=m×(2-0)×(2-

),m=

,
因此抛物线的解析式为:y=

x
2-

x…①
将C
2点的坐标代入①中可得:

×

-

×

=

≠1
因此:A,A
2,C,C
2四点不可能在同一条抛物线上.
分析:(1)由图可知点M应该是△ABC的重心,可依据平面直角坐标系中,三角形重心的坐标是三角形三顶点的算术平均数来求出重心M的坐标;
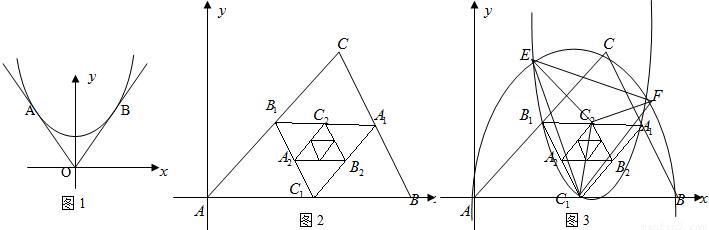
(2)可先根据A、B、C三点的坐标和中位线定理求出A
1、B
1、C
1三点坐标,然后用待定系数法分别求出两条抛物线的解析式;
(3)由于抛物线同时过E、F两点,可联立(2)中两个抛物线的解析式,然后得出一个关于x的一元二次方程,求出的两个解便是E、F点的坐标.然后求出C
2的坐标,如果C2的横坐标大于或小于△EFC
1的所有顶点横坐标,则说明C
2在△EFC1外,如果不是这样,则E、F和C
1坐标都知道了,则根据两点式方程求出△EFC
1三边所在直线的方程,将C2的横坐标分别代入这三个直线方程,
①如果求出的结果全大于或小于C
2的纵坐标,则说明C
2在△EFC
1外;
②如果求出的结果中有一至两个等于C
2的纵坐标,则说明C
2在△EFC
1的边上,甚至顶点上;
③如果求出的结果不全大于或小于C
2的纵坐标,则说明C
2在△EFC
1内.
(4)先用三点的坐标确定一个抛物线的解析式,然后将剩下的一点代入抛物线中即可判断出四点是否在同一抛物线上.
点评:本题着重考查了待定系数法求二次函数解析式、中位线定理、三角形重心等知识点,综合性强.能力要求高.考查学生数形结合的数学思想方法.


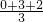 ,
, ),
), ,
, );
); ,1),B1(1,1),C1(
,1),B1(1,1),C1( ,0),
,0),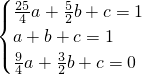
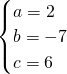
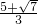 ,x=
,x=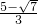
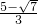 ,
, ),F(
),F(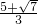 ,
,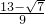 )
) ,1)
,1) ,0)(2,2)(
,0)(2,2)( ,1),
,1), ),
), ),m=
),m= ,
, x2-
x2- x…①
x…① ×
× -
- ×
× =
= ≠1
≠1