
 如图,有一抛物线拱桥,已知水位线在AB位置时,水面的宽为
如图,有一抛物线拱桥,已知水位线在AB位置时,水面的宽为 m,水位上升4m就到达警戒线CD,这时水面的宽为
m,水位上升4m就到达警戒线CD,这时水面的宽为 m,若洪水到来时,水位以每小时0.5m的速度上升,测水过警戒线后几小时淹没到拱桥顶端M处?
m,若洪水到来时,水位以每小时0.5m的速度上升,测水过警戒线后几小时淹没到拱桥顶端M处?科目:初中数学 来源: 题型:
 如图,有一抛物线拱桥,已知水位线在AB位置时,水面的宽为4
如图,有一抛物线拱桥,已知水位线在AB位置时,水面的宽为4| 6 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
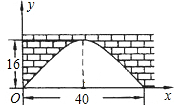 如图,有一座拱桥洞呈抛物线形状,这个桥洞的最大高度为16m,跨度为40m,现把它的示意图放在如图的平面直角坐标系中,则抛物线对应的函数关系式为
如图,有一座拱桥洞呈抛物线形状,这个桥洞的最大高度为16m,跨度为40m,现把它的示意图放在如图的平面直角坐标系中,则抛物线对应的函数关系式为| 1 |
| 25 |
| 1 |
| 25 |
查看答案和解析>>
科目:初中数学 来源:2013届江苏省盐城市第一初级中学教育集团九年级下学期调研考试数学试卷(带解析) 题型:填空题
如图,有一座拱桥洞呈抛物线形状,这个桥洞的最大高度为16 m,跨度为40 m,现把它的示意图放在如图的平面直角坐标系中,则抛物线对应的函数关系式为 .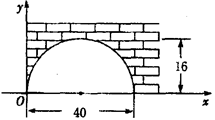
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省盐城市教育集团九年级下学期调研考试数学试卷(解析版) 题型:填空题
如图,有一座拱桥洞呈抛物线形状,这个桥洞的最大高度为16 m,跨度为40 m,现把它的示意图放在如图的平面直角坐标系中,则抛物线对应的函数关系式为 .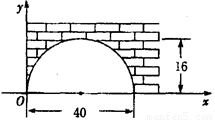
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com