
| A. | 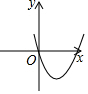 | B. | 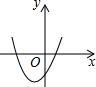 | C. | 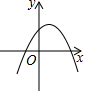 | D. | 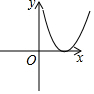 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
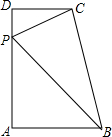 如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7;在AD上能找均一点P,使三角形PAB和三角形PCD相似?若能,共有几个符合条件的点P?并求相应PD的长,若不能,说明理由.
如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7;在AD上能找均一点P,使三角形PAB和三角形PCD相似?若能,共有几个符合条件的点P?并求相应PD的长,若不能,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
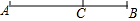 如图,点C在线段AB上,$\frac{AC}{AB}$=$\frac{CB}{AC}$,AB=1,AC=x,则x满足方程(整理成一般形式):x2+x-1=0,解之可求得线段AC=$\frac{-1+\sqrt{5}}{2}$,∴$\frac{AC}{AB}$=$\frac{-1+\sqrt{5}}{2}$=0.618.(精确到0.001)
如图,点C在线段AB上,$\frac{AC}{AB}$=$\frac{CB}{AC}$,AB=1,AC=x,则x满足方程(整理成一般形式):x2+x-1=0,解之可求得线段AC=$\frac{-1+\sqrt{5}}{2}$,∴$\frac{AC}{AB}$=$\frac{-1+\sqrt{5}}{2}$=0.618.(精确到0.001)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com