
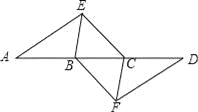
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
【答案】(1)证明见试题解析;(2)4.
【解析】试题分析:(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.
试题解析:(1)∵AB=DC,∴AC=DB,
在△AEC和△DFB中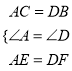 ,∴△AEC≌△DFB(SAS),
,∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF,∴EC∥BF,∴四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,∵AD=10,DC=3,AB=CD=3,
∴BC=10﹣3﹣3=4,∵∠EBD=60°,∴BE=BC=4,
∴当BE="4" 时,四边形BFCE是菱形,
故答案为:4.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
求:
(1)转动转盘,转出的数字大于3的概率是多少;
(2)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
(1)当四边形ABCD分别是菱形、矩形、平行四边形时,相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:

(2)反之,当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时,相应的原四边形ABCD必须满足怎样的条件?
当 时,四边形EFGH是矩形;当 时四边形EFGH是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
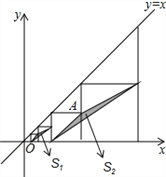
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京时间2011年3月11日,日本近海发生9.0级强烈地震.本次地震导致地球当天自转快了0.0000016秒.这里的0.0000016秒请你用科学记数法表示为秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是【 】

A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标都在格点上,且△A1B1C1与△ABC关于原点O成中心对称,C点坐标为(-2,1)。
(1)请直接写出A1的坐标 ;并画出△A1B1C1.
(2)P(a,b)是△ABC的AC边上一点,将△ABC平移后点P的对称点P'(a+2,b﹣6),请画出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为计算简便,把(-2.4)-(-4.7)-(+0.5)+(+3.4)+(-3.5)写成省略加号的和的形式,并按要求交换加数的位置正确的是( ).
A. -2.4+3.4-4.7-0.5-3.5
B. -2.4+3.4+4.7+0.5-3.5
C. -2.4+3.4+4.7-0.5-3.5
D. -2.4+3.4+4.7-0.5+3.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com