
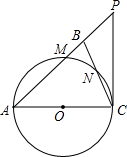
 (2012•广安)如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(2012•广安)如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.| 5 |
| ||
| 5 |
| DC |
| BC |
| DC | ||
2
|
| ||
| 5 |

| 5 |
| ||
| 5 |
| DC |
| BC |
| DC | ||
2
|
| ||
| 5 |
| CN |
| cos∠ACN |
| CN |
| sin∠BCP |
| ||||
|
| BD |
| CP |
| AD |
| AC |
| 20 |
| 3 |
| AC2+CP2 |
| 25 |
| 3 |
| 20 |
| 3 |
| 25 |
| 3 |


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
 (2012•广安)如图,把抛物线y=
(2012•广安)如图,把抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
| 27 |
| 2 |
| 27 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•广安)如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
(2012•广安)如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(| 2 |
| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•广安)如图,已知双曲线y=
(2012•广安)如图,已知双曲线y=| k |
| x |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com