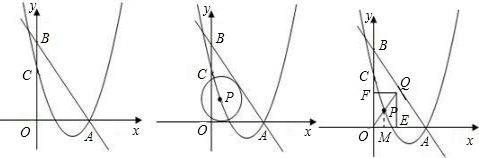
解:(1)B(0,4),OB=4,OA=3,OC=3,
直线解析式为:

,
抛物线的解析式为:y=x
2-4x+3;
(2)若⊙P与直线AB及x轴都相切,
则点P在∠BAO或它的外角的平分线所在的直线上.
①设∠BAO的角平分线交y轴于D,过D作DH⊥AB于H,
则DH=DO=m,BD=4-m,AH=AO=3,BH=5-3=2
在Rt△BHD中,BD
2=BH
2+DH
2即(4-m)
2=m
2+2
2,
解得:

即D(0,1.5)
则直线AD的解析式为:
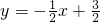
,
将其与抛物线的解析式y=x
2-4x+3联立解得:
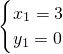
,
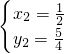
,
即P(

,

)
②作∠BAO外角的平分线交y轴于G,
则AG⊥AD于A,则△DOA∽△AOG,故OG=2OA=6
即G(0,-6)直线DG解析式为:y=2x-6
将其与抛物线的解析式y=x
2-4x+3联立解得:
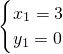
,
综上所述:存在点P(

,

),使⊙P与直线AB及x轴都相切
(3)
过P作PM⊥x轴于M,显然PM是Rt△OQE的中位线,即OE=2OM=2|x|,QE=2PM
点P在抛物线x
2-4x+3上,则P(x,x
2-4x+3),QE=2PM=2|x
2-4x+3|
①当x<0时,x
2-4x+3>0,OE=-2x,y=2[-2x+2(x
2-4x+3)]=4x
2-20x+12
②当1<x<3时,x
2-4x+3<0,y=2[2x-2(x
2-4x+3)]=-4x
2+20x-12
③当0<x<1或x>3时,x
2-4x+3>0,y=2[2x+2(x
2-4x+3)]=4x
2-12x+12
分析:①先确定A,B,C的坐标再来求解析式.②由切线长定理知P点在∠BAO的平分线上或它的外角平分线上.
点评:点在图象上则它的坐标满足图象的解析式,分类讨论的思想的应用.

 ,过点A的抛物线交y轴与点C,且OA=OC,并以直线x=2为对称轴,点P是抛物线上的一个动点.
,过点A的抛物线交y轴与点C,且OA=OC,并以直线x=2为对称轴,点P是抛物线上的一个动点.
 ,
,
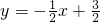 ,
,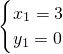 ,
,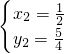 ,
, ,
, )
)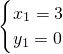 ,
, ,
, ),使⊙P与直线AB及x轴都相切
),使⊙P与直线AB及x轴都相切


 阅读快车系列答案
阅读快车系列答案 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式