
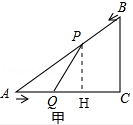
��ͼ�ף��ڡ�ABC�У���ACB=90�㣬AC=4cm��BC=3cm�������P�ɵ�B������BA�������A�����˶���ͬʱ��Q�ɵ�A������AC�������C�����˶������ǵ��ٶȾ�Ϊ1cm/s������PQ�����˶�ʱ��Ϊt��s����0��t��4��������������⣺
��1�����APQ�����ΪS����tΪ��ֵʱ��Sȡ�����ֵ��S�����ֵ�Ƕ��٣�
��2����ͼ�ң�����PC������PQC��QC���ۣ��õ��ı���PQP��C�����ı���PQP��CΪ����ʱ����t��ֵ����
��3����tΪ��ֵʱ����APQ�ǵ��������Σ�
(1)��tΪ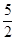 ��ʱ��S���ֵΪ
��ʱ��S���ֵΪ cm2;
cm2;
���ı���PQP��CΪ����ʱ��t��ֵ��s��
��tΪ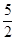 s��
s��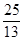 s��
s��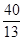 sʱ����APQ�ǵ��������Σ�
sʱ����APQ�ǵ��������Σ�
�������������
��1������P��PH��AC��H���ɡ�APH�ס�ABC���ó� =
=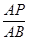 ���Ӷ����AB���ٸ���
���Ӷ����AB���ٸ���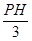 =
=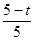 ���ó�PH=3��
���ó�PH=3�� t�����AQP�����Ϊ��
t�����AQP�����Ϊ�� AQ•PH=
AQ•PH= t��3��
t��3�� t�����������������ɵó��𰸣�
t�����������������ɵó��𰸣�
��2������PP�佻QC��E�����ı���PQP��CΪ����ʱ���ó���APE�ס�ABC��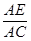 =
=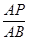 �����AE=��
�����AE=��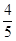 t+4���ٸ���QE=AE��AQ��QE=
t+4���ٸ���QE=AE��AQ��QE= QC�ó���
QC��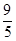 t+4=��
t+4=�� t+2������t���ɣ�
t+2������t���ɣ�
��3���ɣ�1��֪��PD=�� t+3���루2��ͬ���ã�QD=��
t+3���루2��ͬ���ã�QD=��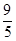 t+4���Ӷ����PQ=
t+4���Ӷ����PQ= ��
��
�ڡ�APQ�У�������������ۣ��ٵ�AQ=AP����t=5��t���ڵ�PQ=AQ���� =t���۵�PQ=AP����
=t���۵�PQ=AP���� =5��t���ٷֱ���㼴��
=5��t���ٷֱ���㼴��
���������
�⣺��1����ͼ�ף�����P��PH��AC��H��
�ߡ�C=90�㣬
��AC��BC��
��PH��BC��
���APH�ס�ABC��
�� =
=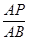 ��
��
��AC=4cm��BC=3cm��
��AB=5cm��
��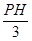 =
=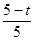 ��
��
��PH=3�� t��
t��
���AQP�������
S= ��AQ��PH=
��AQ��PH= ��t����3��
��t����3�� t��=��
t��=��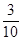 ��t��
��t��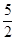 ��2+
��2+ ��
��
�൱tΪ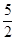 ��ʱ��S���ֵΪ
��ʱ��S���ֵΪ cm2��
cm2��
��2����ͼ�ң�����PP�䣬PP�佻QC��E��
���ı���PQP��CΪ����ʱ��PE��ֱƽ��QC����PE��AC��QE=EC��
���APE�ס�ABC��
��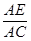 =
=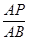 ��
��
��AE=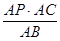 =
=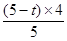 =��
=��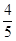 t+4
t+4
QE=AE��AQ�T��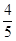 t+4��t=��
t+4��t=��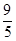 t+4��
t+4��
QE= QC=
QC= ��4��t��=��
��4��t��=�� t+2��
t+2��
�ੁ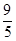 t+4=��
t+4=�� t+2��
t+2��
��ã�t= ��
��
��0�� ��4��
��4��
�൱�ı���PQP��CΪ����ʱ��t��ֵ�� s��
s��
��3���ɣ�1��֪��
PD=�� t+3���루2��ͬ���ã�QD=AD��AQ=��
t+3���루2��ͬ���ã�QD=AD��AQ=��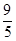 t+4
t+4
��PQ= =
=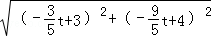 =
=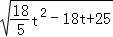 ��
��
�ڡ�APQ�У�
�ٵ�AQ=AP����t=5��tʱ����ã�t1=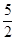 ��
��
�ڵ�PQ=AQ���� =tʱ����ã�t2=
=tʱ����ã�t2=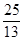 ��t3=5��
��t3=5��
�۵�PQ=AP���� =5��tʱ����ã�t4=0��t5=
=5��tʱ����ã�t4=0��t5=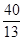 ��
��
��0��t��4��
��t3=5��t4=0�������⣬��ȥ��
�൱tΪ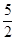 s��
s��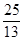 s��
s��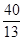 sʱ����APQ�ǵ��������Σ�
sʱ����APQ�ǵ��������Σ�
���㣺�������ۺ���.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
����ͼ��n+1������Ϊ2�ĵ���ֱ��������б����ͬһֱ���ϣ����B2D1C1����Ӱ���֣������ΪS1����B3D2C2�����ΪS2��������Bn+1DnCn�����ΪSn����S2��__________��Sn��__________�����ú�n��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���ڳ�Ϊ8 ����Ϊ4
����Ϊ4 �ľ����У���ȥһ�����Σ�ʹ�����µľ��Σ�ͼ����Ӱ���֣���ԭ�������ƣ������¾��ε������
�ľ����У���ȥһ�����Σ�ʹ�����µľ��Σ�ͼ����Ӱ���֣���ԭ�������ƣ������¾��ε������  .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪��Rt��A��BC���Rt��ABC����A��C��B=��ACB=90�㣬��A��BC��=��ABC=60�㣬Rt��A��BC����Ƶ�B��ת������ת������ֱ��CC���AA���ཻ�ڵ�D��
��1����ͼ1��ʾ������C����AB����ʱ���ж��߶�AD���߶�A��D֮���������ϵ����֤����Ľ��ۣ�
��2����Rt��A��BC����ͼ1��λ����ת��ͼ2��λ��ʱ����1���еĽ����Ƿ����������������֤����������������˵�����ɣ�
��3����Rt��A��BC����ͼ1��λ�ð�˳ʱ�뷽����ת���ǣ�0��ܦ���120�㣩����A��C�䡢A��������һ��ֱ����ʱ����ֱ��д����ת�ǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ������ֽ����һ�������ɰ���С���㣮
��1����ͬһ����ֽ�У�������С����ͼ����ԭ��O��ת180���õ���ͼ����
��2����ͬһ����ֽ�У����� ����Ҳ࣬��ԭС����ͼ��ԭ��OΪλ�����ķŴ�ʹ���ǵ�λ�Ʊ�Ϊ1��2�������Ŵ��С�����ͼ����
����Ҳ࣬��ԭС����ͼ��ԭ��OΪλ�����ķŴ�ʹ���ǵ�λ�Ʊ�Ϊ1��2�������Ŵ��С�����ͼ����
|

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���ڡ�ABC�У�AB=AC����ABΪֱ������O����BC�ڵ�D������OD������D����O�����ߣ���AB�ӳ����ڵ�E����AC�ڵ�F��
��1����֤��OD��AC��
��2����AB=10�� ʱ����AF��BE�ij���
ʱ����AF��BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���ڡ�ABC�У�AB=4��AC=3��D��E�ֱ���AB��AC�ϵĶ��㣬�ڱ�AC��ȡһ��E��ʹA��D��E������ɵ����������ABC���ƣ�
��1����AD=2ʱ����AE�ij���
��2����AD=3ʱ����AE�ij���
��3��ͨ����������Ľ���㷢����ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������ABCD�У�BEƽ�֡�DBC�ҽ�CD���ڵ�E������BCE�Ƶ�C˳ʱ����ת����DCF��λ�ã����ӳ�BE��DF�ڵ�G.
(1)��֤����BDG�ס�DEG��
(2)��EG��BG��4����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪:��ͼ���ڡ�ABC�У�AB=AC,��A=36��,��ABC��ƽ���߽�AC��D��
��1����֤����ABC�ס�BCD��
��2����BC��2����AB�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com