练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个三角形的三边长为5、10、m，则m的取值范围是_______________.

    【答案】5＜m＜15

    【解析】试题分析：三角形的第三边必须满足大于两边之差，小于两边之和，则5＜m＜15．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD中，对角线AC上有一点P，连接BP、DP，过点P作PE⊥PB交CD于点E，连接BE．

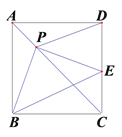
    （1）求证：BP=EP；

    （2）若CE=3，BE=6，求∠CPE的度数；

    （3）探究AP、PC、BE之间的数量关系，并给予证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在四边形ABCD中，AB=CD，要使四边形ABCD是中心对称图形，只需添加一个条件，这个条件可以是　 ▲ 　．（只要填写一种情况）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线（b、c是常数，且c＜0）与x轴交于A、B两点（点A在点B的左侧），与y轴的负半轴交于点C，点A的坐标为（-1,0）．

    （1）b=______，点B的横坐标为_______（上述结果均用含c的代数式表示）；

    （2）连结BC，过点A作直线AE//BC，与抛物线交于点E．点D是x轴上一点，坐标为（2,0），当C、D、E三点在同一直线上时，求抛物线的解析式；

    （3）在（2）的条件下，点P是x轴下方的抛物线上的一动点，连结PB、PC．设△PBC的面积为S．

    ①求S的取值范围；

    ②若△PBC的面积S为正整数，则这样的△PBC共有_____个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

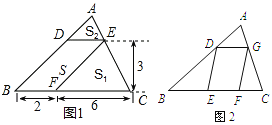
    【题目】问题背景（1）如图1，△ABC中，DE∥BC分别交AB，AC于D，E两点，过点E作EF∥AB交BC于点F．请按图示数据填空：△EFC的面积__________，△ADE的面积______________．

    探究发现（2）在（1）中，若BF=m，FC=n，DE与BC间的距离为．请证明．

    拓展迁移（3）如图2，□DEFG的四个顶点在△ABC的三边上，若△ADG、△DBE、△GFC的面积分别为3、7、5，试利用（2）中的结论求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知三角形的三条中位线的长分别为5cm、6cm、10cm，则这个三角形的周长是_____cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠BAC=90°，BE平分∠ABC，AM⊥BC于点M，AD平分∠MAC，交BC于点D，AM交BE于点G．

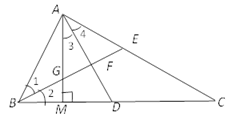
    求证：(1) ∠BAM=∠C;

    (2)判断直线BE与线段AD之间的关系，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）

    A. 2x2·4x2 =8x2 B. x5÷x-1=x4 C. （x4）4=x16 D. （-3x2）3=-9x6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（　　）

    A. a2+a3＝2a5B. a6÷a2＝a3

    C. 2a23a3＝6a5D. （2ab2）3＝6a3b6

    查看答案和解析>>

    同步练习册答案