
分析 (1)根据题意可知乙比甲每小时快20千米,从而可以可以列出相应的方程,求出甲乙的速度;
(2)根据(1)中的答案可以求得总的路程,由题意可知相遇前和相遇后相离20千米,从而可以解答本题.
解答 解:(1)设甲的速度为x千米/时,
4(x+20)=3(x+x+20)
解得,x=10,
∴x+20=30
即甲的速度为10千米/时,乙的速度为30千米/时;
(2)设经过y小时后两人相距20千米,
4×30-20=y(10+30)或4×30+20=y(10+30)
解得,y=2.5或y=3.5,
即经过2.5小时或3.5小时后两人相距20千米.
点评 本题考查一元一次方程的应用,解答本题的关键是明确题意,找出所求问题需要的条件,列出相应的方程,利用分类讨论的数学思想解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
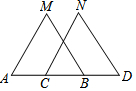 如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )
如图,在△ABM和△CDN中,A,C,B,D在同一条直线上,MB=ND,MA=NC,则下列条件中能判定△ABM≌△CDN的是( )| A. | ∠MAB=∠NCD | B. | ∠MBA=∠NDC | C. | AC=BD | D. | AM∥CN |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
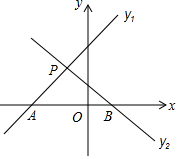 如图,已知直线y1=k1x+m和直线y2=k2x+n交于点P(-1,2),则关于x的不等式(k1-k2)x>-m+n的解是( )
如图,已知直线y1=k1x+m和直线y2=k2x+n交于点P(-1,2),则关于x的不等式(k1-k2)x>-m+n的解是( )| A. | x>2 | B. | x>-1 | C. | -1<x<2 | D. | x<-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 立方根是它本身的数只能是0和1 | |
| B. | 如果一个数有立方根,那么这个数也一定有平方根 | |
| C. | 16的平方根是4 | |
| D. | -2是4的一个平方根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
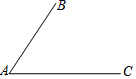 如图,已知线段AB,AC
如图,已知线段AB,AC查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
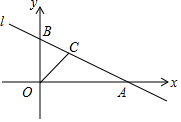 如图,直线l:y=-0.5x+2与x轴、y轴相交于点A,B.OC是∠ABO的角平分线.
如图,直线l:y=-0.5x+2与x轴、y轴相交于点A,B.OC是∠ABO的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com