
【题目】如图,![]() 中,
中,![]() ,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度
,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度![]() 当点M第一次到达B点时,M、N同时停止运动.
当点M第一次到达B点时,M、N同时停止运动.![]() 点M、N运动几秒后,M、N两点重合?
点M、N运动几秒后,M、N两点重合?![]() 点M、N运动几秒后,可得到等边三角形
点M、N运动几秒后,可得到等边三角形![]() ?
?![]() 当点M、N在BC边上运动时,能否得到以MN为底边的等腰
当点M、N在BC边上运动时,能否得到以MN为底边的等腰![]() ?如存在,请求出此时M、N运动的时间.
?如存在,请求出此时M、N运动的时间.
【答案】(1)点M、N运动12秒后,M、N两点重合;(2)点M、N运动4秒后,可得到等边三角形![]() ;(3)当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.
;(3)当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.
【解析】
(1)根据路程差=12构建方程即可解决问题;
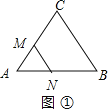
(2)设点M、N运动t秒后,可得到等边三角形△AMN,如图①中,根据AM=AN,构建方程即可解决问题;
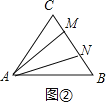
(3)当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,由(1)知12秒时M、N两点重合,恰好在C处,如图②,假设△AMN是等腰三角形,根据CN=BN,构建方程即可解决问题.
![]() 设点M、N运动x秒后,M、N两点重合,
设点M、N运动x秒后,M、N两点重合,
![]() ,
,
解得:![]() ;
;
![]() 点M、N运动12秒后,M、N两点重合.
点M、N运动12秒后,M、N两点重合.
![]() 设点M、N运动t秒后,可得到等边三角形
设点M、N运动t秒后,可得到等边三角形![]() ,如图
,如图![]()
![]() ,
,![]() ,
,
![]() 三角形
三角形![]() 是等边三角形,
是等边三角形,
![]() ,
,
解得![]() ,
,
![]() 点M、N运动4秒后,可得到等边三角形
点M、N运动4秒后,可得到等边三角形![]() .
.
![]() 当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形,
由![]() 知12秒时M、N两点重合,恰好在C处,
知12秒时M、N两点重合,恰好在C处,
如图![]() ,假设
,假设![]() 是等腰三角形,
是等腰三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
在![]() 和
和![]() 中,
中,
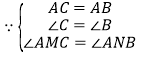 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,![]() 是等腰三角形,
是等腰三角形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
解得:![]() 故假设成立.
故假设成立.
![]() 当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.
当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形,此时M、N运动的时间为16秒.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( ) 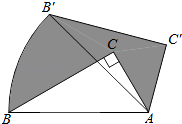
A.![]()
B.![]()
C.![]()
D.π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试结合图示信息回答下列问题:

(1)这32名学生培训前考分的中位数所在的等级是 ,培训后考分的中位数所在的等级是 .
(2)这32名学生经过培训,考分等级“不合格” 的百分比由 下降到 .
(3)估计该校整个八年级中,培训后考分等级为“合格”与“优秀”的学生共有 名.
(4)你认为上述估计合理吗:理由是什么?
答: ,理由: .
查看答案和解析>>
科目:初中数学 来源: 题型:
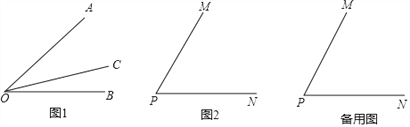
【题目】【探索新知】:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示出所有可能的结果)
【深入研究】:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”;
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.

组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com