
分析 根据A、B、C、D四点在抛物线上可用a、b、x4分别表示y1、y2、y3、y4,由AD∥BC知kAD=kBC即$\frac{{y}_{1}-{y}_{4}}{2-{x}_{4}}$=$\frac{{y}_{2}-{y}_{3}}{0-(-2)}$,将y1、y2、y3、y4代入整理后可得${{x}_{4}}^{2}+2{x}_{4}-8$=0,求出x4的值,最后由S△OBD=$\frac{1}{2}$×OB×|xD|计算可得.
解答 解:根据题意知,y1=4a+2b+4,y2=4,y3=4a-2b+4,y4=ax42+bx4+4,
∵AD∥BC,
∴kAD=kBC,即$\frac{{y}_{1}-{y}_{4}}{2-{x}_{4}}$=$\frac{{y}_{2}-{y}_{3}}{0-(-2)}$,
将y1、y2、y3、y4代入得:$\frac{4a+2b+4-a{{x}_{4}}^{2}-b{x}_{4}-4}{2-{x}_{4}}=\frac{4-4a+2b-4}{2}$,
整理,得:${{x}_{4}}^{2}+2{x}_{4}-8$=0,
解得:x4=-4或x4=2(舍),
∴S△OBD=$\frac{1}{2}$×OB×|xD|
=$\frac{1}{2}$×y2×|x4|
=$\frac{1}{2}$×4×4
=8,
故答案为:8.
点评 本题主要考查二次函数图象上点的坐标特征,根据AD∥BC知kAD=kBC结合二次函数图象上点的坐标求得x4的值是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度AB长12米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ac<bc | B. | a2<b2 | C. | a+1<b+1 | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
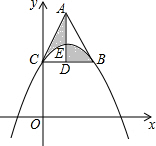 如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.
如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com