练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：=　      　


    2


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    分解因式:  _________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直线与半径的圆O相交，且点O到直线的距离为6，则的取值范围是（    ）

    A、          B、           C、         D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：


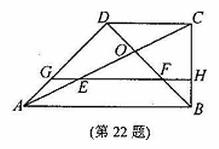
    在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，对角线AC与BD相交于

    点O，线段OA，OB的中点分别为E，F。 （1）求证：△FOE≌△DOC；

    （2）求tan∠BOC的值；  （3）设△AGE, △EFO,△BFH的面积分别为S1，S2, S3,

    求S1： S2： S3 的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （    ）

    A．     B．0<    C．      D．0<

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，射线PN与等腰梯形ABCD的两边AB,CD分别交于点M,N，且AD∥PN, PM=1cm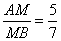，,AB=12cm,AD=3cm,BC=17.4cm,动点Q从P出发，沿射线PN以每秒1cm 的速度递右移动，经过t秒，以点Q为圆心，tcm 为半径的圆与等腰梯形ABCD的边相切，请写出t可以取得一切值                   

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，抛物线y＝nx2－11nx＋24n (n＜0) 与x轴交于B、C两点（点B在点C的左侧），抛物线上另有一点A在第一象限内，且∠BAC＝90°．

    （1）填空：点B的坐标为（_        ），点C的坐标为（_        ）；

    （2）连接OA，若△OAC为等腰三角形．

    ①求此时抛物线的解析式；

    ②如图2，将△OAC沿x轴翻折后得△ODC，点M为①中所求的抛物线上点A与点C两点之间一动点，且点M的横坐标为m，过动点M作垂直于x轴的直线l与CD交于点N，试探究：当m为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．

     


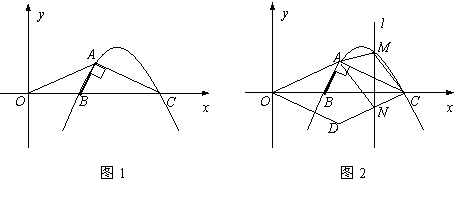    查看答案和解析>>

    科目：初中数学 来源： 题型：


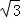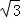    已知代数式(x-2)2-2(x+)(x-)-11

    (1)化简该代数式；

    （2）有人不论x取何值该代数式的值均为负数，你认为这一观点正确吗？请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如右图，在ΔABC中，M、N分别是AB、AC的中点，且∠A +∠B=136°，则∠AN M=          °

     


    查看答案和解析>>

    同步练习册答案