解:(1)证明:∵AB=BC,∠A=36°,∴∠ABC=∠C=72°。
又∵BE平分∠ABC,∴∠ABE=∠CBE=36°。
∴∠BEC=180°﹣∠C﹣∠CBE=72°。∴∠ABE=∠A,∠BEC=∠C。
∴AE=BE,BE=BC。∴AE=BC。
(2)证明:∵AC=AB且EF∥BC,∴AE=AF;
由旋转的性质可知:∠E′AC=∠F′AB,AE′=AF′,
∵在△CAE′和△BAF′中,
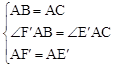
,
∴△CAE′≌△BAF′。∴CE′=BF′。
(3)存在CE′∥AB。
由(1)可知AE=BC,所以,在△AEF绕点A逆时针旋转过程中,E点经过的路径(圆弧)与过点C且与AB平行的直线l交于M、N两点,
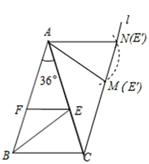
如图:①当点E的像E′与点M重合时,则四边形ABCM为等腰梯形,
∴∠BAM=∠ABC=72°,又∠BAC=36°。
∴α=∠CAM=36°。
②当点E的像E′与点N重合时,
由AB∥l得,∠AMN=∠BAM=72°,
∵AM=AN,∴∠ANM=∠AMN=72°。
∴∠MAN=180°﹣2×72°=36°。
∴α=∠CAN=∠CAM+∠MAN=72°。
∴当旋转角为36°或72°时,CE′∥AB。


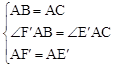 ,
,


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案 = 。
= 。


