
| 1 | 3 |
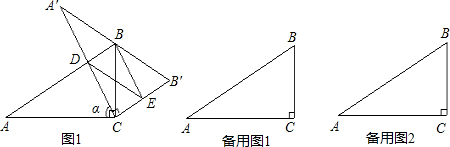
 解:(1)当A′B′过点B时,α=60°;
解:(1)当A′B′过点B时,α=60°;| CD |
| CA′ |
| CE |
| CB′ |

| CD |
| CA |
| CE |
| CB |
| 3 |
| ||
| 2 |
| AD |
| AC |
| BE |
| BC |
| x | ||
|
| BE |
| 1 |
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
-
| ||||
| 6 |
| 1 |
| 3 |
-
| ||||
| 6 |
| ||
| 6 |

| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||||
| 6 |
| 1 |
| 3 |
| ||||
| 6 |
| ||
| 6 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形:
14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形:查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
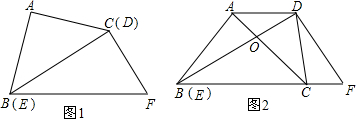
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(
如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com