
 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=| 底边 |
| 腰 |
| BC |
| AB |
| 4 |
| 5 |
| 10 |
| 1 |
| 1 |
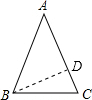 (3)如图,过B作BD⊥AC于D.
(3)如图,过B作BD⊥AC于D.| AD |
| AB |
| 4 |
| 5 |
| BD2+CD2 |
| 10 |
| BC |
| AB |
| ||
| 5 |


科目:初中数学 来源: 题型:
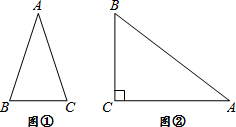 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰=| BC |
| AB |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:2012届福建永安九年级学业质量检测考试数学试卷(带解析) 题型:解答题
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边长与腰长的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA= 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
【小题1】计算:sad60°= ▲
【小题2】对于0°<A<90°,∠A的正对值sadA的取值范围是 ▲ ;
【小题3】如图2,已知△DEF中,∠E=90°,cosD= ,试求sadD的值。
,试求sadD的值。
查看答案和解析>>
科目:初中数学 来源:2012届安徽马鞍山含山一中九年级第二学期数学月考试卷(带解析) 题型:解答题
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)sad60°= .
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是 .
(3)如图②,已知sinA=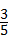 ,其中∠A为锐角,试求sadA的值.
,其中∠A为锐角,试求sadA的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年安徽马鞍山含山一中九年级第二学期数学月考试卷(解析版) 题型:解答题
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad),如图①,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=底边/腰= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
(1)sad60°= .
(2)对于0°<A<180°,∠A的正对值sadA的取值范围是 .
(3)如图②,已知sinA=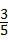 ,其中∠A为锐角,试求sadA的值.
,其中∠A为锐角,试求sadA的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com