
【题目】平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动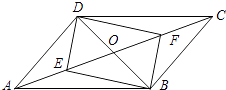
(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=18cm,当运动时间t为多少时,以D、E、B、F为顶点的四边形为矩形.
【答案】
(1)
解:四边形DEBF是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形
(2)
解:根据题意得:AE=CF=2tcm或18﹣2tcm,
∵四边形DEBF是平行四边形,
∴当EF=BD时,四边形DEBF为矩形.
即AC﹣AE﹣CF=BD或AE+CF﹣AC=EF,
∴18﹣2t﹣2t=10或2t+2t﹣18=10,
解得:t=2或t=7
∴当运动时间t为2s或7s时,四边形DEBF为矩形
【解析】(1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:18﹣2t﹣2t=10,继而求得答案.
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质和矩形的判定方法的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】十九大传递出许多值得我们关注的数据,如全国注册志愿团体近38万个.数据38万用科学记数法表示为( )
A.38×104B.3.8×105C.3.8×106D.0.38×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于![]() GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
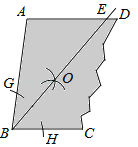
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国首艘国产航母于2018年4月26日正式下水,排水量约为65000吨,将65000用科学记数法表示为( )
A.6.5×10-4B.6.5×104C.-6.5×104D.0.65×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( ) 
A.2 ![]()
B.2
C.4 ![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、G分别是正方形ABCD的边CD、BC上的点,连接AE、AG分别交对角线BD于点P、Q.若∠EAG=45°,BQ=4,PD=3,则正方形ABCD的边长为( ) 
A.6 ![]()
B.7
C.7 ![]()
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com