
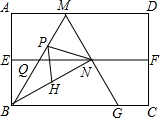
 ��ͼ���ı���ABCD�Ǿ���ֽƬ��AB=2�����۾���ֽƬABCD��ʹAD��BC�غϣ��ۺ�ΪEF��չƽ���ٹ���B�۵�����ֽƬ��ʹ��A����EF�ϵĵ�N���ۺ�BM��EF�ཻ�ڵ�Q���ٴ�չƽ������BN��MN���ӳ�MN��BC�ڵ�G�������½��ۣ�
��ͼ���ı���ABCD�Ǿ���ֽƬ��AB=2�����۾���ֽƬABCD��ʹAD��BC�غϣ��ۺ�ΪEF��չƽ���ٹ���B�۵�����ֽƬ��ʹ��A����EF�ϵĵ�N���ۺ�BM��EF�ཻ�ڵ�Q���ٴ�չƽ������BN��MN���ӳ�MN��BC�ڵ�G�������½��ۣ����� �����ȸ���EF��ֱƽ��AB���ɵ�AN=BN��Ȼ������۵������ʣ��ɵ�AB=BN���ݴ��жϳ���ABNΪ�ȱ������Σ������жϳ���ABN=60�㣻
�����ȸ��ݡ�ABN=60�㣬��ABM=��NBM�������ABM=��NBM=30�㣻Ȼ����Rt��ABM�У�����AB=2�����AM�Ĵ�С���ɣ�
�۸��ݡ�ABM=��MBN=30�㣬��BNM=��BAM=90�㣬�Ƶá�MBG=��BMG=��BGM=60�㣬�����Ƶá�BMG�ǵȱ������Σ�
�����ȸ��ݡ�BMG�ǵȱ������Σ���N��MG���е㣬�жϳ�BN��MG���������BN�Ĵ�С��Ȼ�����E���H�����BM�ƿɵ�PH=PE�����P��Q�غ�ʱ��PN+PH=PN+PE=EN���ݴ����PN+PH����Сֵ�Ƕ��ټ��ɣ�
��� �⣺����ͼ1������AN��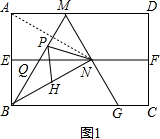
��EF��ֱƽ��AB��
��AN=BN��
�����۵������ʣ��ɵ�
AB=BN��
��AN=AB=BN��
���ABNΪ�ȱ������Σ�
���ABN=60�㣬��PBN=60���2=30�㣬
�����ۢ���ȷ��
�ڡߡ�ABN=60�㣬��ABM=��NBM��
���ABM=��NBM=60���2=30�㣬
��AM=AB•tan30��=2��$\frac{\sqrt{3}}{3}$��
�����ۢڲ���ȷ��
�ۡߡ�ABM=��MBN=30�㣬��BNM=��BAM=90�㣬
���BMG=��BNM-��MBN=90��-30��=60�㣬
���MBG=��ABG-��ABM=90��-30��=60�㣬
���BGM=180��-60��-60��=60�㣬
���MBG=��BMG=��BGM=60�㣬
���BMGΪ�ȱ������Σ�
�����ۢ���ȷ��
�ܡߡ�BMG�ǵȱ������Σ���N��MG���е㣬
��BN��MG����BN=BG•sin60��=$\frac{4\sqrt{3}}{3}$��
����������֪E���H�����BM�Գƣ���PH=PE��
��P��Q�غ�ʱ��PN+PH��ֵ��С����ʱPN+PH=PN+PE=EN��
��EN=$\sqrt{B{N}^{2}-B{E}^{2}}$=$\sqrt{{2}^{2}-��2��2��^{2}}$��
��PN+PH=$\sqrt{3}$��
��PN+PH����Сֵ��$\sqrt{3}$��
�����ۢ���ȷ��
�ʴ�Ϊ���٢ۢܣ�
���� ��1��������Ҫ�����˼��α任�ۺ��⣬�����˷������������������˿ռ��������������������ν�Ϸ�����Ӧ�ã�Ҫ�������գ�
��2����������˵ȱ������ε��ж������ʵ�Ӧ�ã��Լ����ε����ʺ�Ӧ�ã�Ҫ�������գ�
��3������������۵������ʺ�Ӧ�ã��Լ����Ҷ�����Ӧ�ã�Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6x3+1 | B�� | 6x3-3 | C�� | 6x3-3x2 | D�� | 6x3+3x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
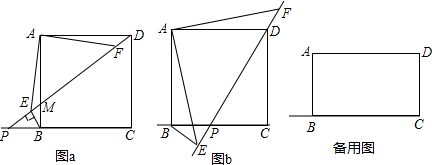
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����г���ţ�̵�������� | B�� | ����ȫ����Сѧ����������� | ||
| C�� | ����ijƷ�Ƶ��ݵ�ʹ������ | D�� | ���麽��ɻ��㲿���Ƿ�ϸ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com