
【题目】如图,已知A、B是反比例函数y= ![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P纵坐标原点O出发,沿O→A→B→C匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形OMPN的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
A.
B.
C.
D.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论: ①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( ) 
A.直线的一部分
B.圆的一部分
C.双曲线的一部分
D.抛物线的一部分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( ) 
A.极差是47
B.众数是42
C.中位数是58
D.每月阅读数量超过40的有4个月
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“自驾游”已成为人们出游的重要方式.“五一”节,林老师驾轿车从舟山出发,上高速公路途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到舟山. 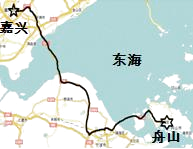
(1)求舟山与嘉兴两地间的高速公路路程;
(2)两座跨海大桥的长度及过桥费见下表:
大桥名称 | 舟山跨海大桥 | 杭州湾跨海大桥 |
大桥长度 | 48千米 | 36千米 |
过桥费 | 100元 | 80元 |
我省交通部门规定:轿车的高速公路通行费y(元)的计算方法为:y=ax+b+5,其中a(元/千米)为高速公路里程费,x(千米)为高速公路里程(不包括跨海大桥长),b(元)为跨海大桥过桥费.若林老师从舟山到嘉兴所花的高速公路通行费为295.4元,求轿车的高速公路里程费a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼,有关成本、销售情况如下表:
养殖种类 | 成本(万元/亩) | 销售额(万元/亩) |
甲鱼 | 2.4 | 3 |
桂鱼 | 2 | 2.5 |
(1)2010年,王大爷养殖甲鱼20亩,桂鱼10亩,求王大爷这一年共收益多少万元?(收益=销售额﹣成本)
(2)2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元.若每亩养殖的成本、销售额与2010年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
(3)已知甲鱼每亩需要饲料500kg,桂鱼每亩需要饲料700kg,根据(2)中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需要全部饲料比原计划减少了2次,求王大爷原定的运输车辆每次可装载饲料多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是%;
(2)本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是%;
(3)家庭用水量的中位数落在组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=6,AC=8,BC=10,D是△ABC内部或BC边上的一个动点(与B、C不重合),以D为顶点作△DEF,使△DEF∽△ABC(相似比k>1),EF∥BC.
(1)求∠D的度数;
(2)若两三角形重叠部分的形状始终是四边形AGDH.
①如图1,连接GH、AD,当GH⊥AD时,请判断四边形AGDH的形状,并证明;
②当四边形AGDH的面积最大时,过A作AP⊥EF于P,且AP=AD,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com