
分析 (1)把b=2,c=-3代入函数解析式,求二次函数的最小值;
(2)根据当c=10时,若在函数值y=l的情况下,只有一个自变量x的值与其对应,得到x2+bx+5=1有两个相等是实数根,求此时二次函数的解析式;
(3)当c=b2时,写出解析式,分三种情况进行讨论即可.
解答 解:(1)当b=2,c=-3时,二次函数的解析式为y=x2+2x-3=(x+1)2-4,
故当x=-1时,二次函数取得最小值-4;
(2)当c=10时,二次函数的解析式为y=x2+bx+10,
由题意得,x2+bx+10=1有两个相等是实数根,
∴△=b2-36=0,
解得b1=6,b2=-6,
∴二次函数的解析式y=x2+6x+10,y=x2-6x+10;
(3)当c=b2时,二次函数解析式为y═x2+bx+b2,
图象开口向上,对称轴为直线x=-$\frac{b}{2}$,
①当-$\frac{b}{2}$<b,即b>0时,
在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而增大,
∴当x=b时,y=b2+b•b+b2=3b2为最小值,
∴3b2=21,解得b1=-$\sqrt{7}$(舍去),b2=$\sqrt{7}$;
②当b≤-$\frac{b}{2}$≤b+3时,即-2≤b≤0,
∴x=-$\frac{b}{2}$,y=$\frac{3}{4}$b2为最小值,
∴$\frac{3}{4}$b2=21,解得b1=-2$\sqrt{7}$(舍去),b2=2$\sqrt{7}$(舍去);
③当-$\frac{b}{2}$>b+3,即b<-2,
在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而减小,
故当x=b+3时,y=(b+3)2+b(b+3)+b2=3b2+9b+9为最小值,
∴3b2+9b+9=21.解得b1=1(舍去),b2=-4;
∴b=$\sqrt{7}$时,解析式为:y=x2+$\sqrt{7}$x+7
b=-4时,解析式为:y=x2-4x+16.
综上可得,此时二次函数的解析式为y=x2+$\sqrt{7}$x+7或y=x2-4x+16.
点评 本题考查了二次函数的最值:当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,因为图象有最低点,所以函数有最小值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$;当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,因为图象有最高点,所以函数有最大值,当x=-$\frac{b}{2a}$时,y=$\frac{4ac-{b}^{2}}{4a}$;确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
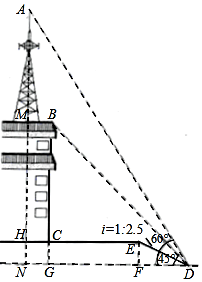 如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)
如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73供选用,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
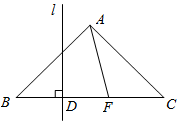 如图,等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点F是边BC上不与点B,C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$-1.
如图,等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点F是边BC上不与点B,C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{2}$或$\sqrt{2}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 班级 | 平均分 | 众数 | 方差 |
| 甲 | 101 | 90 | 2.65 |
| 乙 | 102 | 87 | 2.38 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com