Question

在△ABC中，已知∠CAB=60°，D，E分别是边AB，AC上的点，且∠AED=60°，ED+DB=CE，∠CDB=2∠CDE，则∠DCB=

1. A.
   15°
2. B.
   20°
3. C.
   25°
4. D.
   30°

Answer 1

B
分析：此题要通过构造全等三角形来解；过B作DE的平行线，交AC于F；由于∠AED=∠CAB=60°，因此△ADE是等边三角形，则∠BDE=120°，联立∠CDB、∠CDE的倍数关系，即可求得∠CDE的度数；然后通过证△EDC≌△FCB，得到∠CDE=∠DCB+∠DCE，联立由三角形的外角性质得到的∠CDE+∠DCE=∠ADE=60°，即可求得∠DCB的度数．
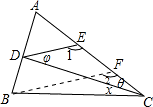
解答：解：∠CAB=60°，∠AED=60°，
∴△ADE是正三角形．
作BF∥DE交AC于F，
∴△ABF∽△ADE，
∴△ADF是等边三角形，
则BD=EF，
从而EC=DE+BD=AB=BF，DE=FC，
又∠1=∠2=120°，
∴△EDC≌△FCB，
∴θ+x=φ；
∵∠CDB=2φ，∠BDE=120°，
∴φ=40°，
θ+x=40°；
∵θ+φ=θ+40°=60°
∴θ=20°，
得：x=20°．
故选B．
点评：此题考查了全等三角形的判定和性质、三角形的外角性质等知识，正确画出图形，并构造出全等三角形是解决问题的关键．