
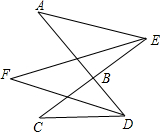
 小明在课外学习时遇到一道难题:“已知:AD和CE交于B,EF,DF分别为∠AEC,∠ADC的角平分线,且∠A=60°,∠C=70°,求∠F的度数.”小明苦思冥想后有了头绪,于是他设∠AEF=∠FEC=x,∠ADF=∠FDC=y,请你帮他继续解决,求出∠F的度数为________.
小明在课外学习时遇到一道难题:“已知:AD和CE交于B,EF,DF分别为∠AEC,∠ADC的角平分线,且∠A=60°,∠C=70°,求∠F的度数.”小明苦思冥想后有了头绪,于是他设∠AEF=∠FEC=x,∠ADF=∠FDC=y,请你帮他继续解决,求出∠F的度数为________.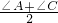 ,
,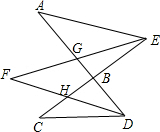 设∠AEF=∠FEC=x,∠ADF=∠FDC=y,
设∠AEF=∠FEC=x,∠ADF=∠FDC=y,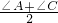 ,
, (60°+70°)=65°.
(60°+70°)=65°.

科目:初中数学 来源: 题型:
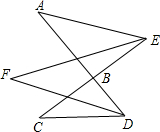 小明在课外学习时遇到一道难题:“已知:AD和CE交于B,EF,DF分别为∠AEC,∠ADC的角平分线,且∠A=60°,∠C=70°,求∠F的度数.”小明苦思冥想后有了头绪,于是他设∠AEF=∠FEC=x,∠ADF=∠FDC=y,请你帮他继续解决,求出∠F的度数为
小明在课外学习时遇到一道难题:“已知:AD和CE交于B,EF,DF分别为∠AEC,∠ADC的角平分线,且∠A=60°,∠C=70°,求∠F的度数.”小明苦思冥想后有了头绪,于是他设∠AEF=∠FEC=x,∠ADF=∠FDC=y,请你帮他继续解决,求出∠F的度数为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com