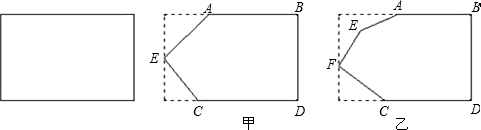
解:(1)过E作EF∥AB(如图甲).
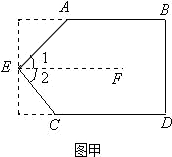
∵原四边形是长方形,
∴AB∥CD,
又∵EF∥AB,
∴CD∥EF(平行于同一条直线的两条直线互相平行).
∵EF∥AB,
∴∠A+∠1=180°(两直线平行,同旁内角互补).
∵CD∥EF,
∴∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠A+∠1+∠2+∠C=360°,
又∵∠1+∠2=∠AEC,
∴∠A+∠AEC+∠C=360°.
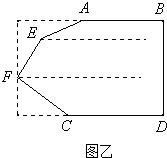
(2)过点E、F分别作AB的平行线(如图乙),
用上面的方法可得∠A+∠E+∠F+∠C=3×180°=540°.
(3)剪出5个角,共剪四刀,其和为720°,即(5-1)×180°=720°;
由此可得一般规律:剪出n个角,这n个角的和是(n-1)×180°.
分析:(1)过点E作EF∥AB,再根据两直线平行,同旁内角互补即可得到三个角的和等于180°的2倍;
(2)分别过E、F作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;
(3)根据前两问的剪法,剪出5个角,需要4刀,n个角需要(n-1)刀,剪几刀就是180°的几倍,算出即可.
点评:作平行线并利用两直线平行,同旁内角互补是解本题的关键,总结规律求解是本题的难点.