
 如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )| A. |  | B. |  | C. | 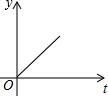 | D. |  |
分析 作AD⊥BC于D,如图,设点F运动的速度为1,BD=m,根据等腰三角形的性质得∠B=∠C,BD=CD=m,当点F从点B运动到D时,如图1,利用正切定义即可得到y=tanB•t(0≤t≤m);当点F从点D运动到C时,如图2,利用正切定义可得y=tanC•CF=-tanB•t+2mtanB(m≤t≤2m),即y与t的函数关系为两个一次函数关系式,于是可对四个选项进行判断.
解答 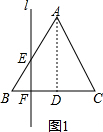 解:作AD⊥BC于D,如图,设点F运动的速度为1,BD=m,
解:作AD⊥BC于D,如图,设点F运动的速度为1,BD=m,
∵△ABC为等腰三角形,
∴∠B=∠C,BD=CD,
当点F从点B运动到D时,如图1,
在Rt△BEF中,∵tanB=$\frac{EF}{BF}$,
∴y=tanB•t(0≤t≤m);
当点F从点D运动到C时,如图2,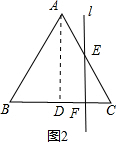
在Rt△CEF中,∵tanC=$\frac{EF}{CF}$,
∴y=tanC•CF
=tanC•(2m-t)
=-tanB•t+2mtanB(m≤t≤2m).
故选B.
点评 本题考查了动点问题的函数图象:利用三角函数关系得到两变量的函数关系,再利用函数关系式画出对应的函数图象.注意自变量的取值范围.


科目:初中数学 来源: 题型:解答题
 如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,PO•OQ=y.
如图,在多边形ABCDE中,∠A=∠AED=∠D=90°,AB=5,AE=2,ED=3,过点E作EF∥CB交AB于点F,FB=1,过AE上的点P作PQ∥AB交线段EF于点O,交折线BCD于点Q,设AP=x,PO•OQ=y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )
如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )| A. | 35° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,EF=2,那么AH等于6.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,EF=2,那么AH等于6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为$\frac{15}{4}$.
如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为$\frac{15}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.
如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
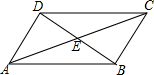 如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )| A. | 6 | B. | 12 | C. | 20 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com