
 如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$.
如图,在正方形ABCD内有一折线段,其中AE丄EF,EF丄FC,并且AE=3,EF=4,FC=5,则正方形ABCD的外接圆的半径是4$\sqrt{5}$. 分析 首先连接AC,则可证得△AEM∽△CFM,根据相似三角形的对应边成比例,即可求得EM与FM的长,然后由勾股定理求得AM与CM的长,进而得到AC的长,在Rt△ABC中,由AB=AC•sin45°,即可求出正方形的边长
解答 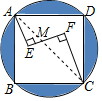 解:连接AC,
解:连接AC,
∵AE丄EF,EF丄FC,
∴∠E=∠F=90°,
∵∠AME=∠CMF,
∴△AEM∽△CFM,
∴$\frac{AE}{CF}$=$\frac{EM}{FM}$,
∵AE=3,EF=4,FC=5,
∴$\frac{EM}{FM}$=$\frac{3}{5}$,
∴EM=1.5,FM=2.5,
在Rt△AEM中,AM=$\sqrt{A{E}^{2}+E{M}^{2}}$=$\frac{3\sqrt{5}}{2}$,
在Rt△FCM中,CM=$\sqrt{C{F}^{2}+F{M}^{2}}$=$\frac{5\sqrt{5}}{2}$,
∴AC=4$\sqrt{5}$,
∴正方形ABCD的外接圆的半径是4$\sqrt{5}$,
故答案为:4$\sqrt{5}$.
点评 此题考查了相似三角形的判定与性质,正方形的性质以及勾股定理的应用.此题综合性较强,解题时要注意数形结合思想的应用.


 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{25}$ | D. | $\frac{56}{65}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
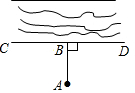 某工程队计划把河水引到水池A中,他们先过A点作AB⊥CD,垂足为B,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是( )
某工程队计划把河水引到水池A中,他们先过A点作AB⊥CD,垂足为B,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是( )| A. | 两点之间线段最短 | B. | 经过两点有且只有一条直线 | ||
| C. | 垂直定义 | D. | 垂线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
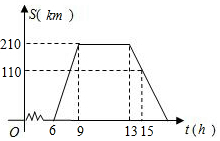 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
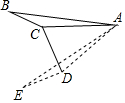 如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.
如图,在△ABC中,∠ACB=α(90°<α<180°),将△ABC绕着点A逆时针旋转2β(0°<β<90°)后得△AED,其中点E、D分别和点B、C对应,联结CD,如果CD⊥ED,请写出一个关于α与β的等量关系的式子α+β=180°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
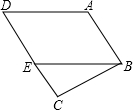 如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com