
分析 (1)要证明方程有两个不相等的实数根,即证明△>0即可.△=[-(k+2)]2-4(2k-1)=k2-6k+13=(k-2)2+4,因为(k-2)2≥0,可以得到△>0;
(2)将x=1代入方程x2-(k+1)x+2k-3=0,求出k的值,进而得出方程的解,探讨得出等腰三角形的周长.
解答 (1)证明:∵△=[-(k+2)]2-4(2k-1)=k2-4k+8=(k-2)2+4,
而(k-2)2≥0,
∴△>0.
∴对任意实数k,方程有两个不相等的实数根;
(2)解:∵方程的一个根是1,
∴12-(k+2)+2k-1=0,
解得:k=2,
∴原方程为:x2-4x+3=0,
解得:x1=1,x2=3.
方程的另一个根是3,
等腰三角形的三边长为3,3,1,周长为3+3+1=7.
点评 此题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.同时考查了一元二次方程的解的定义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
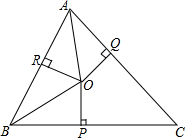 如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com