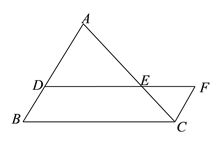
【题目】如图，已知△ABC中，点D、E分别在边AB和AC上，DE∥BC，点F是DE延长线上的点， 
，联结FC，
（1）求证：AB//CF；
（2）若
，FC=6，求AB的长．
【答案】见解析
【解析】试题分析:(1) 因为DE∥BC,根据平线分线段成比例可证得, 
,因为
,
所以
,又因为∠AED=∠CEF,可证△AED∽△CEF,可证得: ∠ADE=∠F,利用内错角相等两直线平行可判定,（2）因为DE∥BC, AB//CF,可判定四边形BDFC是平行四边形,所以FC=BD,根据△AED∽△CEF,可得
,根据
可得: 
,即
,因为FC=6,所以AD=12,所以AB=18.
解：（1）∵
,
∴
,
∵
,
∴
,
∴AB//CF ,
（2）∵DE∥BC,AB//CF,
∴四边形DBCF是平行四边形,
∴BD=CF=6,
∵AB//CF,
∴
,
∴AD=12,
∴AB=18,
或：先证明△FCE∽△ABC,得
，得
,
所以AB=18 .
科目：初中数学 来源： 题型：
【题目】（本小题满分9分）
已知：△ABC是任意三角形．
（1）如图1所示，点M、P、N分别是边AB、BC、CA的中点．求证：∠MPN=∠A．
（2）如图2所示，点M、N分别在边AB、AC上，且
， 
，点P1、P2是边BC的三等分点，你认为∠MP1N+∠MP2N=∠A是否正确？请说明你的理由．
（3）如图3所示，点M、N分别在边AB、AC上，且
， 
，点P1、P2、……、P2009是边BC的2010等分点，则∠MP1N+∠MP2N+……+∠MP2009N=____________．
（请直接将该小问的答案写在横线上．）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D，E为BC边的中点，连接DE、OE.
(1)求证：DE是⊙O的切线；
(2)填空：
①当∠CAB＝ 时，四边形AOED是平行四边形；
②连接OD，在①的条件下探索四边形OBED的形状为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若直线y=-2x+1经过（3，y1）,(-2,y2)，则y1 ,y2的大小关系是（ ）
A、 y1＞y2 B、 y1＜y2 C、 y1 ＝y2 D、 无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店有两个进价不同的计算器都卖了64元，其中一个盈利60%，另一个亏损20%，在这次买卖中，这家商店（ ）
A.不赔不赚
B.赚了32元
C.赔了8元
D.赚了8元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com