
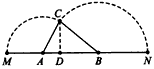
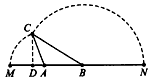
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1,以A 为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x。
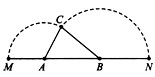
| 解:(1)在△ABC中,∵AC=1,AB=x,BC=3-x, ∴ 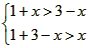 , ,解得1<x<2; (2)①若AC为斜边,则1=x2+(3-x)2,即x2-3x+4=0,无解; ②若AB为斜边,则x2=(3-x)2+1,解得x= 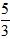 , ,满足1<x<2; ③若BC为斜边,则(3-x)2=1+x2,解得x= 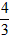 ,满足1<x<2, ,满足1<x<2,∴x= 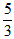 或x= 或x=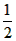 ; ;(3)在△ABC中,作CD⊥AB于D,设CD=h,△ABC的面积为S,则S= 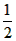 xh, xh,①如图甲所示,若点D在线段AB上, 则 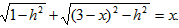 , ,∴(3-x)2-h2=x2-2x 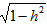 +1-h2,即x +1-h2,即x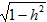 =3x-4, =3x-4,∴x2(1-h2)=9x2-24x+16,即x2h2=-8x2+24x-16, ∴S2= 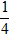 x2h2=-2x2+6x-4=-2 x2h2=-2x2+6x-4=-2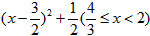 , ,当x= 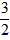 时(满足 时(满足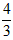 ≤x<2),S2取最大值 ≤x<2),S2取最大值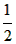 ,从而S取最大值 ,从而S取最大值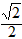 , ,②如图乙所示,若点D在线段MA上,则 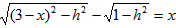 , ,同理可得,S2= 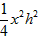 =-2x2+6x-4=-2(x- =-2x2+6x-4=-2(x- )2+ )2+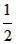 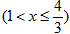 , ,易知此时S< 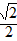 , ,综合①②得,△ABC的最大面积为 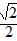 。 。 |
  |


科目:初中数学 来源: 题型:
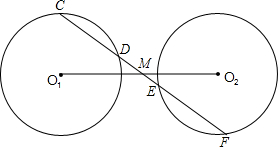 助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)
助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
18、如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知P、Q是△ABC的边BC上的两点,BQ=CP,若不增加任何字母与辅助线,要使△ABP≌△ACQ,则还需增加一个条件是
如图,已知P、Q是△ABC的边BC上的两点,BQ=CP,若不增加任何字母与辅助线,要使△ABP≌△ACQ,则还需增加一个条件是查看答案和解析>>
科目:初中数学 来源: 题型:
 几何基础问题
几何基础问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com