练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知如图，一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点，不等式ax+b＞$\frac{k}{x}$的解集为（　　）
    A．x＜-3B．x＜-3或x＞1C．-3＜x＜0或x＞1D．-3＜x＜1

    分析 观察函数图象得到当-3＜x＜0或x＞1时，一次函数图象都在反比例函数图象上方，即有ax+b＞$\frac{k}{x}$．

    解答 解：不等式ax+b＞$\frac{k}{x}$的解集为-3＜x＜0或x＞1．
    故选C．

    点评 本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了观察函数图象的能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本Q（元）与月产销量y（个）满足如下关系：
    月产销量y（个）…160200240300…
    每个玩具的固定成本Q（元）…60484032…
    （1）每月产销量y（个）与销售单价x（元）之间的函数关系式为y=-2x+860；从上表可知，每个玩具的固定成本Q（元）与月产销量y（个）之间满足反比例函数关系式，求出Q与y之间的关系式；
    （2）若每个玩具的固定成本为30元，求它的销售单价是多少元？
    （3）若该厂这种玩具的月产销量不超过400个，求此时销售单价最低为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，BE=DF．
    （1）求证：AE=AF；
    （2）连接AC交EF于点O，延长OC至点M，使OM=OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

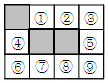    5．在由相同的小正方形组成的3×4的网格中，有3个小正方形已经涂黑，请你再涂黑一个小正方形，使涂黑的四个小正方形构成的图形为轴对称图形，则还需要涂黑的小正方形序号是（　　）
    A．①或②B．③或⑥C．④或⑤D．③或⑨

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，在楼顶点A处观察旗杆CD测得旗杆顶部C的仰角为30°，旗杆底部D的俯角为45°．已知楼高AB=9m，则旗杆CD的高度为（　　）
    A．$（9+\sqrt{3}）$mB．$（9+3\sqrt{3}）$mC．9$\sqrt{3}$mD．12$\sqrt{3}$m

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．据统计，2015年广州地铁日均客运量约为659万．将659万用科学记数法表示为（　　）
    A．0.659×107B．6.59×106C．6.59×107D．659×104

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图是由6个大小相同的小正方体摆成的立体图形，它的左视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列图形中既是轴对称图形又是中心对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知，如图，在平面直角坐标系xOy中，点A、B、C分别为坐标轴上的三个点，且OA=1，OB=3，OC=4．
    （1）求经过A、B、C三点的抛物线的解析式及顶点坐标；
    （2）在抛物线上是否存在一点P，使△ACP的面积等于△ACB的面积？若存在，请求出点P的坐标；若不存在，请说明理由；
    （3）在平面直角坐标系xOy中是否存在一点Q，使得以点A、B、C、Q为顶点的四边形为菱形？若存在，请求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案