
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
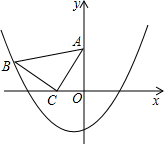 两坐标轴上,点B的坐标为(-3,1),且抛物线y=ax2+ax-4a经过点B.
两坐标轴上,点B的坐标为(-3,1),且抛物线y=ax2+ax-4a经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2009-2010学年天津市河西区九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,将一张直角三角形纸片![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,这时
重合,这时![]() 为折痕,
为折痕,![]() 为等腰三角形;再继续将纸片沿
为等腰三角形;再继续将纸片沿![]() 的对称轴
的对称轴![]() 折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”
折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”
 | |||||
 | 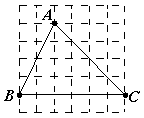 | ||||
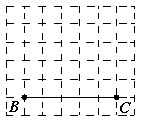
图① 图② 图③
(1)如图②,正方形网格中的![]() 能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
能折叠成“叠加矩形”吗?如果能,请在图②中画出折痕;
(2)如图③,在正方形网格中,以给定的![]() 为一边,画出一个斜三角形
为一边,画出一个斜三角形![]() ,使其顶点
,使其顶点![]() 在格点上,且
在格点上,且![]() 折成的“叠加矩形”为正方形;
折成的“叠加矩形”为正方形;
(3)若一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com