
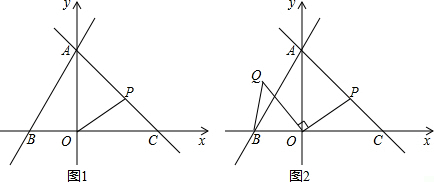
 如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.分析 (1)由A,B的坐标及∠AEO=30°可得OE=3$\sqrt{3}$,即可求出点E的坐标;
(2)分三种情形①当EA=EP时,EP1=EA=EP2=6,求出t.②当PA=PE时,设P3E=P3E=x,在Rt△AOP3中,32+(3$\sqrt{3}$-x)2=x2,x=$2\sqrt{3}$,求出t即可.③当AE=AP时,点P在点Q左边,不符合题意.
(3)本小题分三种情况讨论:①当PA⊥AE时,⊙P与AE相切;②当PA⊥AC时,⊙P与AC相切;③当PB⊥BC时,⊙P与BC相切;分别求出各种情况的t的值.
解答 解:(1)∵A(0,3),B(6,0),
∴OA=3,OB=6,
∵∠AEO=30°,
∴OE=$\sqrt{3}$OA=3$\sqrt{3}$,
∴点E的坐标为($3\sqrt{3}$,0).
(2)如图1中,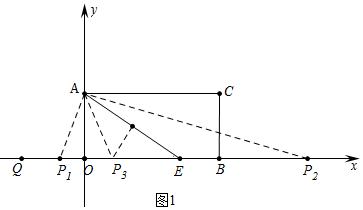
当EA=EP时,EP1=EA=EP2=6,此时t=3$\sqrt{3}$-2或3$\sqrt{3}$+10,
当PA=PE时,设P3E=P3E=x,在Rt△AOP3中,32+(3$\sqrt{3}$-x)2=x2,
∴x=$2\sqrt{3}$,此时t=4+$\sqrt{3}$
当AE=AP时,点P在点Q左边,不符合题意.
综上所述,当△PAE是等腰三角形时,t的值为(3$\sqrt{3}$-2)s或(3$\sqrt{3}+10$)s或(4+$\sqrt{3}$)s.
(3)由题意知,若⊙P与四边形AEBC的边相切,有以下三种情况:
①如图2中,当PA⊥AE时,⊙P与AE相切,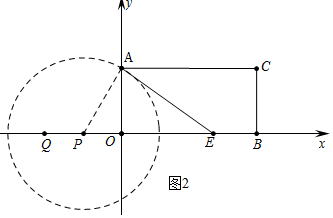
∵∠AEO=30°,AO=3,
∴∠APO=60°,
∴OP=$\sqrt{3}$,
∴QP=QO-PO=4-$\sqrt{3}$,
∵点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=4-$\sqrt{3}$(秒).
②如图3中,当PA⊥AC时,⊙P与AC相切,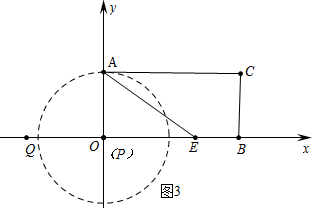
∵QO=4,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位的速度运动,
∴t=4(秒),
③如图4中,当⊙P与BC相切时,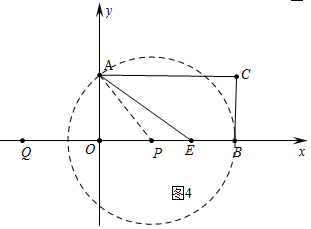
由题意,PA2=PB2=(10-t)2,PO2=(t-4)2.
于是(10-t)2=(t-4)2+32.
解得t=$\frac{25}{4}$(秒),
综上所述,当⊙P与四边形AEBC的边(或边所在的直线)相切时,t的值为(4-$\sqrt{3}$)秒或4秒或$\frac{25}{4}$秒.
点评 本题考查了圆的综合,涉及了圆与直线的位置关系、锐角三角函数的定义及外角的性质,解题的关键是学会用分类讨论的思想思考问题,学会把问题转化为方程解决,属于中考压轴题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
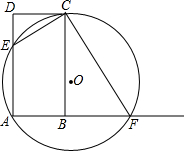 如图,在矩形ABCD中,AB=1,BC=2,点E是AD边上一动点(不与点A,D重合 ),过A、E、C三点的⊙O交AB延长线于点F,连接CE、CF.
如图,在矩形ABCD中,AB=1,BC=2,点E是AD边上一动点(不与点A,D重合 ),过A、E、C三点的⊙O交AB延长线于点F,连接CE、CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com