
(本题12分)△ABC中,∠A,∠B,∠C的对边分别为a,b,c,关于x的方程x2-2ax+b2=0的两根为x1、x2,x轴上两点M、N的坐标分别为(x1,0)、(x2,0),其中M的坐标是(a+c,0);P是y轴上一点,点 。
。

1.(1)试判断△ABC的形状,并说明理由;
2.(2)若S△MNP=3S△NOP, ①求sinB的值; ②判断△ABC的三边长能否取一组适当的值,使△MND是等腰直角三角形?如能,请求出这组值;如不能,请说明理由.
科目:初中数学 来源: 题型:
(本题12分)在梯形ABCD中,AB∥CD,∠BCD=90,且AB=1,BC=2,tan∠ADC=2;对角线相交于O点,等腰直角三角板的直角顶点落在梯形的顶点C上,使三角板绕点C旋转。
(1)当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
(2)在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
 (3)当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=
(3)当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=![]() 时,求PE及DH的长。
时,求PE及DH的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题12分)如图,已知抛物线y=![]() x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y= x+b相交于点B、C,直线y=
x+b相交于点B、C,直线y=![]() x+b与y轴交于点E.
x+b与y轴交于点E.
(1)写出直线BC的解析式;
(2)求△ABC的面积;
(3)若点M在线段AB上以每秒1个单位长度的速度从A向B运动(不与A、B重合),同时,点N在射线BC上以每秒2个单位长度的速度从B向C运动。设运动时间为t秒,请写出△MNB的面积s与t的函数关系式,并求出点M运动多少时间时,△MNB的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
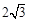 .把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.
.把△ABC放在平面直角坐标系中,使AB的中点位于坐标原点O (如图),△ABC可以绕点O作任意角度的旋转.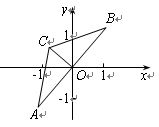
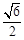 时,求点B的横坐标;
时,求点B的横坐标; 的对称轴经过点C,请你探究:
的对称轴经过点C,请你探究: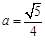 ,
,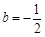 ,
,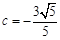 时,A,B两点是否都在这条抛物线上?并说明理由;
时,A,B两点是否都在这条抛物线上?并说明理由; ,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.
,是否存在这样的m的值,使A,B两点不可能同时在这条抛物线上?若存在,直接写出m的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2012届广西省灌阳县八年级上学期期末质量检测数学卷 题型:解答题
( 本题12分) 已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E。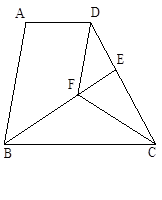
求证:【小题1】(1)△BFC≌△DFC;
【小题2】(2)AD=DE
查看答案和解析>>
科目:初中数学 来源:2010-2011学年上海市考模拟数学试卷 题型:解答题
(本题12分)
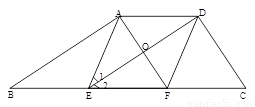
如图,AD//BC,点E、F在BC上,∠1=∠2,AF⊥DE,垂足为点O.
(1)求证:四边形AEFD是菱形;
(2)若BE=EF=FC,求∠BAD+∠ADC的度数;
(3)若BE=EF=FC,设AB = m,CD = n,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com