
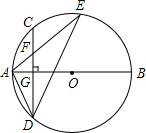
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①利用垂径定理可知$\widehat{AC}$=$\widehat{AD}$,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;②结合CF=2,且$\frac{CF}{FD}$=$\frac{1}{3}$,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=$\frac{\sqrt{5}}{4}$,且∠E=∠ADG,可判断出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7$\sqrt{5}$.
解答 解:①∵AB为直径,AB⊥CD,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠ADF=∠AED,且∠FAD=∠DAE,
∴△ADF∽△AED,
∴①正确;
②∵AB为直径,AB⊥CD,
∴CG=DG,
∵$\frac{CF}{FD}$=$\frac{1}{3}$,且CF=2,
∴FD=6,
∴CD=8,
∴CG=4,
∴FG=CG-CF=4-2=2,
∴②错误;
③在Rt△AGF中,AF=3,FG=2,
∴AG=$\sqrt{A{F}^{2}-F{G}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,且DG=4,
∴tan∠ADG=$\frac{AG}{GD}$=$\frac{\sqrt{5}}{4}$,
∵∠E=∠ADG,
∴tan∠E=$\frac{\sqrt{5}}{4}$,
∴③错误;
④在Rt△ADG中,AG=$\sqrt{5}$,DG=4,
∴AD=$\sqrt{21}$,
∴$\frac{AF}{AD}$=$\frac{3}{\sqrt{21}}$=$\frac{\sqrt{21}}{7}$,
∴△ADF∽△AED中的相似比为$\frac{\sqrt{21}}{7}$,
∴$\frac{{S}_{△ADF}}{{S}_{△AED}}$=($\frac{\sqrt{21}}{7}$)2=$\frac{3}{7}$,
在△ADF中,DF=6,AG=$\sqrt{5}$,
∴S△ADF=$\frac{1}{2}$DF•AG=$\frac{1}{2}$×6×$\sqrt{5}$=3$\sqrt{5}$,
∴$\frac{3\sqrt{5}}{{S}_{△AED}}$=$\frac{3}{7}$,
∴S△ADE=7$\sqrt{5}$,
∴④错误;
∴正确的有①一个.
故选A.
点评 本题主要考查垂径定理、相似三角形的判定和性质及三角函数的定义,由垂径定理得到G是CD的中点是解题的关键,判断③时注意利用等角的三角函数也相等,在判断④时求出相似比是解题的关键.本题所考查知识点较多,综合性较强,解题时注意知识的灵活运用.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:填空题
 如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.
如图,AD与BC交于点E,∠BAC=∠ACD=90°,∠B=45°,∠D=30°,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
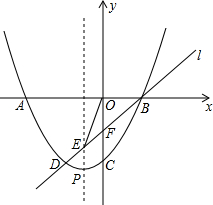 如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.
如图,已知二次函数y=ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C.过点B的直线l与这个二次函数的图象的另一个交点为D,与该图象的对称轴交于点E,与y轴交于点F,且DE:EF:FB=1:1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
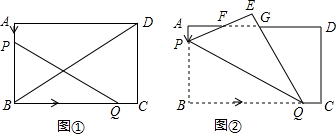 如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).
如图①,已知矩形ABCD中,AB=60cm,BC=90cm.点P从点A出发,以3cm/s的速度沿AB运动:同时,点Q从点B出发,以20cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点同时停止运动.设点P、Q运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
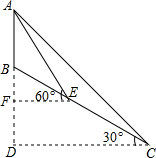 如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.
如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{2}{3}$ | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com