
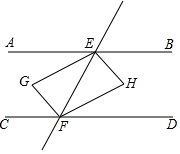
 如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.
如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个. 分析 根据角平分线的定义得到∠AEG=∠GEF=$\frac{1}{2}$∠AEF,根据余角的性质得到∠BEH=∠FEH,于是得到EH平分∠BEF;故①正确,根据平移的性质得到四边形EGFH是平行四边形,根据平行四边形的性质得到EG∥FH,EG=HF;故②正确;根据平行线的性质得到∠AEF=∠DFE,于是得到FH平分∠EFD;故③正确;根据矩形的性质得到∠GFH=90°,故④正确.
解答  解:∵EG平分∠AEF,
解:∵EG平分∠AEF,
∴∠AEG=∠GEF=$\frac{1}{2}$∠AEF,
∵HE⊥GE于E,
∴∠GEH=90°,
∴∠GEF+∠HEF=90°,
∴∠AEG+∠BEH=90°,
∴∠BEH=∠FEH,
∴EH平分∠BEF;故①正确,
∵平移EH恰好到GF,
∴四边形EGFH是平行四边形,
∴EG∥FH,EG=HF;故②正确;
∴∠GEF=∠EFH,
∵AB∥CD,
∴∠AEF=∠DFE,
∵∠GEF=$\frac{1}{2}∠$AEF,
∴∠EFH=$\frac{1}{2}∠$EFD,
∴FH平分∠EFD;故③正确;
∵四边形EGFH是平行四边形,∠GEH=90°,
∴四边形EGFH是矩形,
∴∠GFH=90°,故④正确,
∴正确的结论有4个,
故答案为:4.
点评 本题考查了平移的性质,平行线的性质,角平分线的定义,平行四边形的判定和性质,矩形的判定和性质,熟练掌握平移的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为$\frac{9}{4}$或1.
如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为$\frac{9}{4}$或1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )| A. | 16$\sqrt{3}$ | B. | 24 | C. | 12$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com