练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
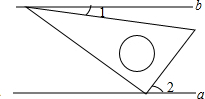
    19．如图，将一块含有60°角的直角三角板的两个顶点放在两条平行的直线a，b上，如果∠2=50°，那么∠1的度数为（　　）
    A．10°B．20°C．30°D．40°

    分析 根据平行线的性质即可得到结论．

    解答 解：如图，过E作EF∥直线a，
    则EF∥直线b，
    ∴∠3=∠1，∠4=∠2，
    ∴∠1=60°-∠2=10°，
    故选A．

    点评 本题考查了平行线的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．下表是世界人口增长趋势数据表：
     年份x 1960 1974 1987 1999 2010
     人口数量y（亿） 30 40 50 60 69
    （1）请你认真研究上面数据表，求出从1960年到2010年世界人口平均每年增长多少亿人；
    （2）利用你在（1）中所得到的结论，以1960年30亿人口为基础，设计一个最能反映人口数量y关于年份x的函数关系式，并求出这个函数的解析式；
    （3）利用你在（2）中所得的函数解析式，预测2020年世界人口将达到多少亿人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．一元一次方程3x-3=0的解是（　　）
    A．x=1B．x=-1C．x=$\frac{1}{3}$D．x=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．二次函数y=ax2+bx+c的图象如图所示，则下列结论不正确的是（　　）
    A．a＜0B．c＞0C．a+b+c＞0D．b2-4ac＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，一次函数y=ax+b（a≠0）的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于A（-3，2），B（2，n）．
    （1）求反比例函数y=$\frac{k}{x}$的解析式；
    （2）求一次函数y=ax+b的解析式；
    （3）观察图象，直接写出不等式ax+b＜$\frac{k}{x}$的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．在下列条件中，能够判定一个四边形是平行四边形的是（　　）
    A．一组对边平行，另一组对边相等
    B．一组对边相等，一组对角相等
    C．一组对边平行，一条对角线平分另一条对角线
    D．一组对边相等，一条对角线平分另一条对角线

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在平面直角坐标系中，已知抛物线C1：y=$\frac{3}{2}{x}^{2}+6x+2$的顶点为M，与y轴相交于点N，先将抛物线C1沿x轴翻折，再向右平移p个单位长度后得到抛物线C2：直线l：y=kx+b经过M，N两点．
    （1）结合图象，直接写出不等式$\frac{3}{2}$x2+6x+2＜kx+b的解集；
    （2）若抛物线C2的顶点与点M关于原点对称，求p的值及抛物线C2的解析式；
    （3）若直线l沿y轴向下平移q个单位长度后，与（2）中的抛物线C2存在公共点，求3-4q的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．
    （1）已知点M，N是线段AB的勾股分割点，若AM=2，MN=3，求BN的长；
    （2）已知点C是线段AB上的一定点，其位置如图2所示，请在BC上画一点D，使C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画一种情形即可）；
    （3）如图3，已知点M，N是线段AB的勾股分割点，MN＞AM≥BN，△AMC，△MND和△NBM均是等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，若AM=4，求△BMG的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．某射击运动员练习时的10次成绩如下：6，7，7，7，8，8，9，9，9，10，则这组数据的方差为1.4．

    查看答案和解析>>

    同步练习册答案