
分析 (1)设商场日盈利达到1200元时,每件商品售价为x元,根据每件商品的盈利×销售的件数=商场的日盈利,列方程求解即可;
(2)根据题意得出盈利与售价之间的关系,进而利用二次函数最值求法求出即可.
解答 解:(1)设每件商品应涨价x元,根据题意得:
(130+x-120)(70-x)=1200,
解得:x1=10,x2=50,
130+10=140,130+50=180
答:每件商品的售价定为140元或180元.
(2)设每件涨价x元,每日销售该商品总的利润为y元,
y=(130+x-120)(70-x)=-x2+60x+700,
当x=$-\frac{b}{2a}=30$时,y最大=1600元,
所以当每件商品的销售价定为160元时,商场销售该商品每日的利润最大,最大利润是1600元.
点评 此题主要考查了二次函数与一元二次方程的应用,根据每件商品的盈利×销售的件数=商场的日盈利,列出方程是关键.


科目:初中数学 来源: 题型:解答题
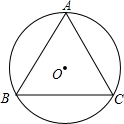 如图,△ABC内接于⊙O,
如图,△ABC内接于⊙O,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
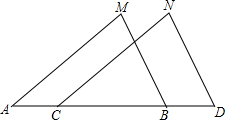 如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,MB∥ND,添加下列条件后,仍不能判定△ABM≌△CDN的是( )| A. | AM=CN | B. | AC=BD | C. | ∠M=∠N | D. | AM∥CN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com