练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．二次函数y=a（x-3）2+4（a≠0）的图象在1＜x＜2这一段位于x轴的上方，在5＜x＜6这一段位于x轴的下方，则a的值为（　　）
    A．1B．-1C．2D．-2

    分析 先根据抛物线的解析式可求得抛物线的对称轴为x=3，由二次函数的对称性可知当4＜x＜5时，函数图象位于x轴的上方，结合题意可知当x=5时，y=0，从而可求得a的值．

    解答 解：∵y=a（x-3）2+4（a≠0），
    ∴抛物线的对称轴为x=3．
    又∵当1＜x＜2时，函数图象位于x轴的上方，
    ∴当4＜x＜5时，函数图象位于x轴的上方．
    又∵当5＜x＜6时，函数图象位于x轴的下方，
    ∴当x=5时，y=0．
    ∴4a+4=0．
    ∴a=-1．
    故选：B．

    点评 本题主要考查的而是二次函数的性质，利用二次函数的性质得到当x=5时，y=0是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．如图，将长方形ABCD沿折痕EF对折，使点C与点A重合，若∠AEB=50°，则∠AFE=65°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，在△ABC中，AB=AC，且AE=AD，∠EDC=α，则∠BAD=（　　）
    A．αB．2αC．3αD．4α

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，已知AB，CD相交于点O，OE⊥CD于O，∠AOC=35°，则∠BOE的度数是（　　）
    A．35°B．55°C．125°D．145°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知抛物线y=ax2+bx+c（c≠0）的对称轴为直线x=1，且经过点P（-1，0），则抛物线与x轴的另一个交点坐标为（3，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=-1，且过点（-3，0），下列说法：
    ①b2-4ac=0；
    ②4a+2b+c＜0；
    ③3a+c=0；
    ④若（-5，y1），（2，y2）是抛物线上的两点，则y1＞y2，
    其中正确的是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

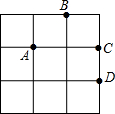    8．如图，在3×3的正方形网格中由四个格点A，B，C，D，以其中一点为原点，网格线所在直线为坐标轴，建立平面直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是（　　）
    A．A点B．B点C．C点D．D点

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，抛物线y=-x2+（1-m）x-m2+12交x轴于点A，交y轴于点B（0，3），顶点C位于第二象限，连结AB，AC，BC．
    （1）求抛物线的解析式；
    （2）在x轴上是否存在点P，使得△PAB的面积等于△ABC的面积？如果存在，求出P点坐标；
    （3）将△ABC沿x轴向右平移t个单位长度（0＜t＜1）时，平移后△ABC与△ABO重叠部分的面积为S，求S与t之间的函数关系式．

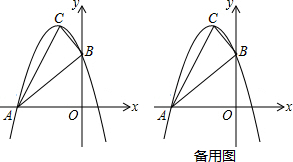
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

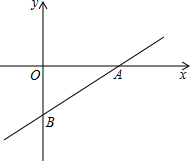    6．如图，直线y=$\frac{3}{4}$x-3交x轴于点A，交y轴于点B．已知x轴上某一点C到直线y=$\frac{3}{4}$x-3的距离为5，则点C的坐标为（$\frac{37}{3}$，0）或（-$\frac{13}{3}$，0）．

    查看答案和解析>>

    同步练习册答案