
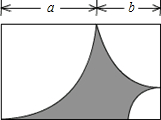
 如图所示,当a=3,b=2时,阴影部分的面积等于________.
如图所示,当a=3,b=2时,阴影部分的面积等于________.科目:初中数学 来源: 题型:
 8、某种蓄电池的电压为定值,使用此电源时,电流I(A)与可变电阻R(Ω)之间的函数关系如图所示,当用电器的电流为10A时,用电器的可变电阻为
8、某种蓄电池的电压为定值,使用此电源时,电流I(A)与可变电阻R(Ω)之间的函数关系如图所示,当用电器的电流为10A时,用电器的可变电阻为查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
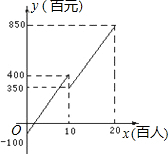 一次时装表演会预算中票价定为每张100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险5000(不列入成本费用),请解答下列问题:
一次时装表演会预算中票价定为每张100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险5000(不列入成本费用),请解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com