
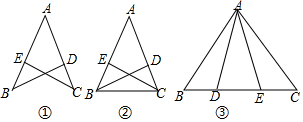
分析 (1)根据全等三角形的判定定理SAS结合给定条件即可得出缺少条件AD=AE,此题得解;
(2)根据全等三角形的判定定理SAS结合给定条件即可得出缺少条件∠DBC=∠ECB,此题得解;
(3)由AD=AE、BD=CE、∠ADB=∠AEC利用全等三角形的判定定理SAS即可证出△ABD≌△ACE,再根据全等三角形的性质即可得出∠C=∠B=40°,结合三角形内角和定理即可得出∠CAE=45°,此题得解.
解答 解:(1)∵∠A=∠A,AB=AC,
∴若要用“SAS”证△ABD≌△ACE,则需添加条件AD=AE.
故答案为:AD;AE.
(2)∵BD=CE,BC=CB,
∴若要用“SAS”证△BDC≌△CEB,则需添加条件∠DBC=∠ECB.
故答案为:∠DBC;∠ECB.
(3)在△ABD和△ACE中,$\left\{\begin{array}{l}{AD=AE}\\{∠ADB=∠AEC}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE(SAS),
∴∠C=∠B=40°,
∴∠CAE=180°-∠AEC-∠C=45°.
故答案为:ABD;ACE;45.
点评 本题考查了全等三角形的判定与性质以及三角形内角和定理,熟练掌握全等三角形的判定定理SAS是解题的关键.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小亮和小颖想用下面的方法测量学校教学楼的高度:如图,小亮蹲在地上,小颖站在小亮和教学楼之间,两人适当调整自己的位置,当楼的顶部M、小颖的头部B及小亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C、D,然后测出两人之间的距离CD=2m,小颖与教学楼之间的距离DN=38m,(C、D、M在同一直线上),小颖的身高BD=1.6m,小亮蹲地观测时眼睛到底面的距离AC=1m.请你根据以上测量数据帮助他们求出教学楼的高度.
小亮和小颖想用下面的方法测量学校教学楼的高度:如图,小亮蹲在地上,小颖站在小亮和教学楼之间,两人适当调整自己的位置,当楼的顶部M、小颖的头部B及小亮的眼睛A恰好在一条直线上时,两人分别标定自己的位置C、D,然后测出两人之间的距离CD=2m,小颖与教学楼之间的距离DN=38m,(C、D、M在同一直线上),小颖的身高BD=1.6m,小亮蹲地观测时眼睛到底面的距离AC=1m.请你根据以上测量数据帮助他们求出教学楼的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AC与BD交于O点,AB∥DC,AB=DC.
如图,AC与BD交于O点,AB∥DC,AB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
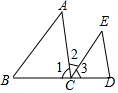 如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.
如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com