
 (x>0,m是常数)的图象经过A(1,4),B(a,b),其中a
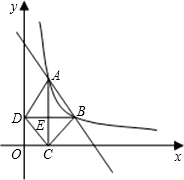
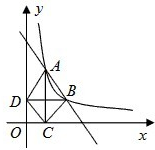
(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a >1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.
>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.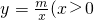 ,m是常数)图象经过A(1,4),
,m是常数)图象经过A(1,4),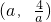 ,D点的坐标为
,D点的坐标为 ,E点的坐标为
,E点的坐标为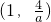 ,
,
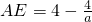 .
.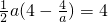 ,
, ;
;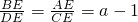 ,
,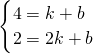 ,
, ,
,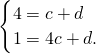 ,
,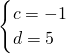 ,
, ,求出反比例函数解析式,利用三角形ABC的面积为4求出a的值,进而求出a的坐标;
,求出反比例函数解析式,利用三角形ABC的面积为4求出a的值,进而求出a的坐标;

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
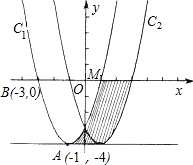 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)查看答案和解析>>
科目:初中数学 来源: 题型:
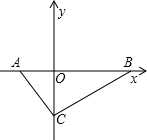 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=| 4 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y=| m |
| x |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 完成下列各题:
完成下列各题:
|
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com