解:(1)抛物线y=ax
2+bx-4a经过A(1,0)、C(0,4)两点,
∴

解得

∴此抛物线的解析式为y=-x
2-3x+4.
(2)∵点D(m,1-m)在抛物线y=-x
2-3x+4上,
∴-m
2-3m+4=1-m,
解之,得m
1=-3,m
2=1.
∵点D在第二象限,
∴D(-3,4).
令y=-x
2-3x+4=0,
得x
1=1,x
2=-4.
∴B(-4,0).
∴∠CBO=45°.
连接DC,

易知DC∥BA,DC⊥CO,DC=3,
∴∠DCB=∠CBO=45°.
∴∠BCD=45°.
过点D作DE⊥BC于E,延长DE交y轴于F,
∴∠D=45°.
∴∠CFE=45°.
∴DE=CE=EF.
∴点F即为点D关于直线BC的对称点.
∴CD=CF=3.
∴F(0,1).
(3)∵∠CDB>90°,∠BCD=45°,
∴∠DBC<45°
∵∠DBP=45°,
∴点P在直线BC下方的抛物线上.
在Rt△DCE中,DC=3,∠DCE=45°,
∴DE=EC=

.
在Rt△BCO中,OB=OC=4,
∴BC=4

.
∴BE=

.
∴在Rt△BDE中,tan∠DBE=

.
∵∠DBP=∠CBO=45°,
∴∠DBC=∠PBO.
∴tan∠DBC=tan∠PBO=

.
过点P作PM⊥x轴于M,
∴在Rt△BDE中,tan∠PBO=

=

.
设PM=3t,则BM=5t,
∴OM=5t-4.
∴P(5t-4,3t).
∴-(5t-4)
2-3(5t-4)+4=3t.
解得t
1=0,t
2=
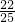
.
∴P(

,

).
分析:(1)由抛物线y=ax
2+bx-4a经过A(1,0)、C(0,4)两点,利用待定系数法即可求得抛物线的解析式;
(2)由点D(m,1-m)在抛物线y=-x
2-3x+4上,即可求得点D的坐标,则可求得∠CBO的度数,然后过点D作DE⊥BC于E,延长DE交y轴于F,又由点F即为点D关于直线BC的对称点,即可求得点F的坐标;
(3)由∠CDB>90°,∠BCD=45°,可得点P在直线BC下方的抛物线上.然后在Rt△DCE中与Rt△BCO中,Rt△BDE中,由三角函数的知识求得∠PBO的正切值,然后过点P作PM⊥x轴于M,在Rt△BDE中,利用三角函数的知识即可求得点P的坐标.
点评:此题考查了待定系数法求二次函数的解析式,点的对称性,直角三角形的性质以及三角函数的知识.此题综合性很强,难度较大,解题的关键是方程思想、转化思想与数形结合思想的应用.

 抛物线y=ax2+bx-4a经过A(1,0)、C(0,4)两点,与x轴交于另一点B.
抛物线y=ax2+bx-4a经过A(1,0)、C(0,4)两点,与x轴交于另一点B.


 .
. .
. .
. .
. .
. =
= .
.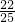 .
. ,
, ).
).



 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.