分析:根据正六边形的性质直接得出其半径和周长,连接正六边形的中心和各顶点,得到六个全等的正三角形,于是可知正六边形的边长等于正三角形的边长,为正六边形的外接圆半径.
解答: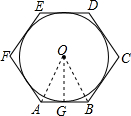
解:如图,连接OA、OB,OG;
∵六边形ABCDEF是边长为1的正六边形,
∴正六边形的周长为:6,
∴△OAB是等边三角形,
∵正六边形的半径为正六边形外接圆半径,
∴正六边形的半径为1,
∴OA=AB=1,
∴OG=OA•sin60°=1×
=
,
∴边长为1的正六边形的内切圆的半径为:
.
故答案为:1,6,
.
点评:本题考查了对正多边形的概念掌握和计算的能力.解答此题要熟悉正多边形的边长、半径、边心距等概念,以及正六边形和正三角形的关系等概念.

 解:如图,连接OA、OB,OG;
解:如图,连接OA、OB,OG;
