
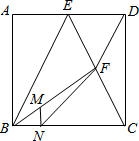
 如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、BF,点M是BF上一点且
如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、BF,点M是BF上一点且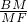 =
= ,过点M做MN⊥BC于点N,连接FN.下列结论中:
,过点M做MN⊥BC于点N,连接FN.下列结论中: AB;④
AB;④ =
= .
. DE=
DE= a,GF=
a,GF= CD=a.再根据正切函数的定义可得tan∠AEB=tan∠GDF=2,则∠AEB=∠GDF,BE∥DF,从而有∠BEF=∠DFE,故②正确;由△EFG≌△CFH,得出FG=FH=a,由MN∥FH,根据平行线分线段成比例定理,可得MN=
CD=a.再根据正切函数的定义可得tan∠AEB=tan∠GDF=2,则∠AEB=∠GDF,BE∥DF,从而有∠BEF=∠DFE,故②正确;由△EFG≌△CFH,得出FG=FH=a,由MN∥FH,根据平行线分线段成比例定理,可得MN= FH=
FH= a,则MN=
a,则MN= AB,故③正确;分别计算S△FMN与S四边形FEBN,即可得出
AB,故③正确;分别计算S△FMN与S四边形FEBN,即可得出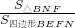 =
=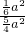 =
= ,故④错误.
,故④错误.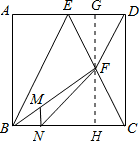 解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形, a,
a, a,
a, DE=
DE= a,GF=
a,GF= CD=a.
CD=a. =
= =2,
=2,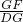 =
=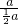 =2,
=2, a.
a. a,
a, a.
a.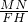 =
=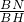 =
=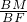 =
= ,
, FH=
FH= a,BN=
a,BN= BH=
BH= a,
a, AB,故③正确;
AB,故③正确; a,
a, MN•NH=
MN•NH= ×
× a×a=
a×a= a2,
a2, •2a•a-
•2a•a- •2a•a-
•2a•a- •
• a•a=
a•a= a2.
a2.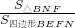 =
=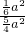 =
= ,故④错误.
,故④错误.

科目:初中数学 来源: 题型:
 ,交BC于点E.
,交BC于点E.| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com