练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图点E在AB上，AC=AD，∠1=∠2。
    （1） △ACE和△ADE全等吗？说明理由；
    （2） 你能判断△CEB和△DEB全等吗？说明理由。
    解：（1）全等；理由“略”
    （2）全等；理由“略”
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知OABC是一张矩形纸片，AB=6．
    （1）如图1，在AB上取一点M，使得△CBM与△CB′M关于CM所在直线对称，点B′恰好在边OA上，且△OB′C的面积为24cm2，求BC的长；
    （2）如图2．以O为原点，OA、OC所在直线分别为x轴、y轴建立平面直角坐标系．求对称轴CM所在直线的函数关系式；
    （3）作B′G∥AB交CM于点G，若抛物线y=
    16
    x2+m过点G，求精英家教网这条抛物线所对应的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源：第2章《二次函数》中考题集（32）：2.3 二次函数的应用（解析版） 题型：解答题

    已知OABC是一张矩形纸片，AB=6．
    （1）如图1，在AB上取一点M，使得△CBM与△CB′M关于CM所在直线对称，点B′恰好在边OA上，且△OB′C的面积为24cm2，求BC的长；
    （2）如图2．以O为原点，OA、OC所在直线分别为x轴、y轴建立平面直角坐标系．求对称轴CM所在直线的函数关系式；
    （3）作B′G∥AB交CM于点G，若抛物线y=x2+m过点G，求这条抛物线所对应的函数关系式．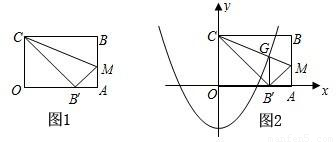

    查看答案和解析>>

    科目：初中数学 来源：第20章《二次函数和反比例函数》中考题集（30）：20.5 二次函数的一些应用（解析版） 题型：解答题

    已知OABC是一张矩形纸片，AB=6．
    （1）如图1，在AB上取一点M，使得△CBM与△CB′M关于CM所在直线对称，点B′恰好在边OA上，且△OB′C的面积为24cm2，求BC的长；
    （2）如图2．以O为原点，OA、OC所在直线分别为x轴、y轴建立平面直角坐标系．求对称轴CM所在直线的函数关系式；
    （3）作B′G∥AB交CM于点G，若抛物线y=x2+m过点G，求这条抛物线所对应的函数关系式．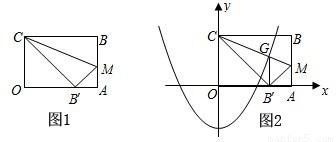

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年浙江省启东市寒假测试数学卷 题型：选择题

    （本小题共6分）

    如图,点E在CD上,点F在BA上,G是AD延长线上一点.

     (1)若∠A=∠1,则可判断_______∥_______,因为________.       

     (2)若∠1=∠_______,则可判断AG∥BC，因为_________.

     (3)若∠2+∠_______=180°,则可判断CD∥AB,因为____________.

     

     

    查看答案和解析>>

    同步练习册答案