
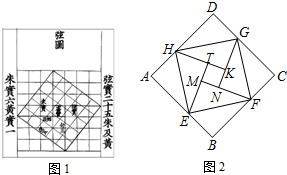
 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图1.图2由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=9,则S2的值是
我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图1.图2由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=9,则S2的值是 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
 如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )A、2
| ||
B、
| ||
C、2
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
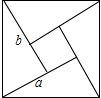 如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=45°,A1、A2、A3、…在射线OA上,B1、B2、B3、…在射线OB上,且A1B1⊥OA,A2B1⊥OA,…AnBn⊥OA; A2B2⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6…).若OA1=1,则AnBn的长是( )
如图,已知∠AOB=45°,A1、A2、A3、…在射线OA上,B1、B2、B3、…在射线OB上,且A1B1⊥OA,A2B1⊥OA,…AnBn⊥OA; A2B2⊥OB,…,An+1Bn⊥OB(n=1,2,3,4,5,6…).若OA1=1,则AnBn的长是( )A、
| ||
B、(
| ||
| C、2n | ||
| D、2n-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )| A、25cm | B、50cm | C、75cm | D、100cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com