Question

【题目】如图，在边长为的正方形中，点在上从向运动，连接交于点．

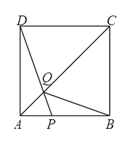
（）试证明：无论点运动到上何处时，都有≌．

（）若点从点运动到点，再继续在上运动到点，在整个运动过程中，当点运动到什么位置时， 恰为等腰三角形．

Answer 1

【答案】（）证明见解析；（）。

【解析】分析：（1）根据正方形的四条边都相等可得AD=AB，对角线平分一组对角可得∠DAQ=∠BAQ=45°，然后利用“边角边”证明△ADQ和△ABQ全等；（2）分①AQ=DQ时，点B、P重合，②AQ=AD时，根据等边对等角可得∠ADQ=∠AQD，再求出正方形的对角线AC的长，再求出CQ，然后根根据两直线平行，内错角相等求出∠CPQ=∠ADQ，从而得到∠CQP=∠CPQ，根据等角对等边可得CP=CQ，从而得到点P的位置，③AD=DQ时，点C、P、Q三点重合．

本题解析：

（）如图，∵在正方形中，无论运动到何处，

都有， ．

∴在和中， ．

∴≌．

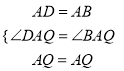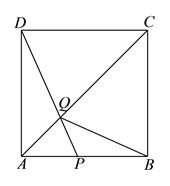
（）为等腰三角形．

如图， 时，此时为正方形．

的中心，此时点与点重合．

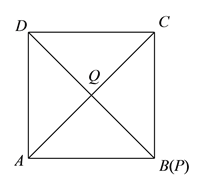
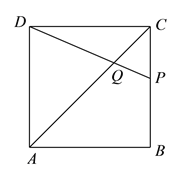
②如图， 时，由等边对等角得： ．

∴， ．

∴

∵

∵

∴

∴．

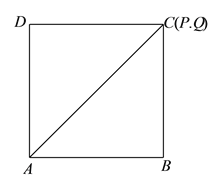
③如图， 时，

此时、、三点重合．

综上所述：当运动到①点位置②处（上）③点位置时， 为等腰三角形．