
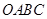 的两顶点
的两顶点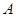 、
、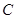 分别在
分别在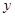 轴、
轴、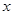 轴的正半轴上,点
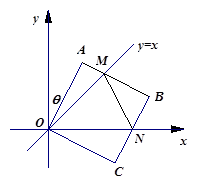
轴的正半轴上,点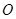 在原点.现将正方形
在原点.现将正方形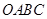 绕
绕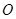 点顺时针旋转,旋转角为θ,当
点顺时针旋转,旋转角为θ,当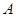 点第一次落在直线
点第一次落在直线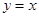 上时停止旋转.旋转过程中,
上时停止旋转.旋转过程中, 边交直线
边交直线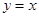 于点
于点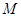 ,
,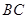 边交
边交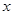 轴于点
轴于点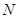 .
.
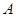 点第一次落在直线
点第一次落在直线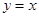 上时,求A、B两点坐标(直接写出结果);
上时,求A、B两点坐标(直接写出结果);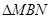 的周长为
的周长为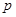 ,在旋转正方形
,在旋转正方形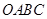 的过程中,
的过程中,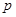 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论. 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.12分 | B.10分 | C.16分 | D.14分 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.甲同学比乙同学先出发半小时 |
| B.乙比甲先到达B地 |
| C.乙在行驶过程中没有追上甲 |
| D.甲的行驶速度比乙的行驶速度慢 |
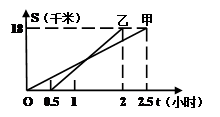
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,L
,L 分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题:
分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系。根据图像,回答下列问题:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com